I remember as a student being asked to estimate in mathematics class on a few occasions. It was either an afterthought from my teachers telling the group to estimate before we do our work to help us with the “reasonableness” of our answers, or during measurement activities where we had to estimate then measure items around the classroom. As a student though, when asked to actually estimate, I always did the calculations or measuring first, then wrote down a number that was near the actual answer as my “estimate”. Was I confusing rounding with estimating? Or was I avoiding thinking???
It might come as a surprise to consider just how much estimating we do outside of school. Within the same day we might determine how much milk to pour on our cereal so it is covered but won’t get soggy, think about how early we need to leave for work to make sure we aren’t late, figure out if we can safely squeeze our car into a parking space, consider how loud to speak to someone across the room, determine an appropriate amount to tip the waitress at dinner, think about if there is enough time during the commercial break to use the restroom so you don’t miss any of your favourite show… Whether we know it or not, nearly every minute of the day, we are estimating about physical spaces and numbers.
In school, however, the practice of estimating is often neglected. Many of our students are estimating all the time without realizing it, but others might not be aware of the mental actions others are doing and don’t engage in the same active thinking processes! Because of this, I believe we should be estimating more than we probably realize. The skill of estimation is directly related to our Number Sense and our Spatial Reasoning, so we need to make estimating a priority!
Kinds of estimating:
Situations in which we estimate involve: computational estimations, measurement estimations, numerosity estimates (how many) and number line estimates. Computational and numerosity estimations are directly related to students’ Number Sense (i.e., size of numbers, doubling, how much more or less…) and often involve students approximating numbers. While estimates involving measurement and number lines involve our students’ Spatial Reasoning (i.e., considering the size and space of objects). However, if we really delve deeply into any of the 4 kinds of estimating, they probably each deal with our Number Sense and each deal with our ability to think Spatially.
Questions that ask students to estimate distance or length:
Take a look at the following 5 questions. Which type of question do you think is most common in school? Which type of question is less common?

For many students, estimating a measurement is about “guessing”, then actually measuring. To a student, the act of estimating becomes useless in this scenario. If they are going to measure anyway, why did they estimate anything? Many of the questions above ask students to go beyond guessing and ask them to develop benchmarks then think about subdividing or iterating those benchmarks. While some of our students will naturally develop these benchmarks and strategies to subdivide/iterate, many others will not without rich tasks and discussions. For these reasons, we likely need to spend more time than we might realize estimating and discussing our strategies / thinking.
Questions that ask students to estimate area:
Take a look at the 5 questions below. Which ones might help your students better understand the concept of area? Which ones might help them consider the attributes of area you want them to notice?
To many students, concepts like area are easy… plug in the numbers to a formula and you get your answer. Estimating, however, requires far more thinking and understanding of the attributes than simple calculations. For this reason, it is probably best if we start by asking our students to estimate well before they are ever given any formulas, and continually as they learn more complicated shapes.
Each of the above problems ask our students to actually consider the size and shape of the things they are thinking about. Hopefully this happens ALL the time as our students learn measurement concepts!
Questions that ask students to estimate angles:
As a student I remember learning types of angles and how to read a protractor – very knowledge based and procedural in nature. However, as a teacher I regularly see students who can easily tell me if an angle is greater or less than 90 degrees, but make seemingly careless mistakes when actually measuring an angle. Personally, I believe that the issue isn’t about students being careless, it is more about a student’s experiences with angles. Specifically, too many students are asked to DO something instead of them being asked to THINK about something when it comes to topics like angles. Above are 5 problems / tasks that ask students to think first by estimating. When the task is about estimating, it adds motivation for students to actually measure to see how close they might be!
Questions that ask students to estimate number or computations:
Look at the 6 problems/tasks below. Which ones do you think are more common in classrooms? Why do you think they are more common? Which ones require your students to consider the space numbers take up? Which ones help our students develop and use their number sense?
When the problems / tasks we give are about estimating, our students think about what they already know and use this as a basis for learning new things. While the aim for many of us is to help our students determine reasonableness for our students’ answers, in real life, estimates are likely good enough most of the time!
We need to estimate more!
Estimating needs to be integrated into more of what we teach, instead of it being an isolated lesson/ concept. Whether teaching probability or time or Geometry or patterns… we need to ask our students to think more before they start doing any calculation!
Special Thanks
Hopefully you have heard of Andrew Stadel’s Estimation 180. This is an easy to use routine that can help us with some of the types of estimation I have talked about here!

One of the best parts about these routines is that it helps students build benchmarks, use number sense, think spatially and consider the importance of a range of reasonable answers instead of just “guessing”.
Jamie Duncan added to the conversation when she shared snapshots of how she helped her students refine their ranges:

After noticing her students’ ranges were quite large, she started asking her students to indicate their “brave” too low and “brave” too high estimates. Ideally we want our students focused on their range of values, not their actual estimate. Focusing on the actual estimate promotes guessing, while focusing on student ranges helps us think more about reasonableness. Brilliant idea!
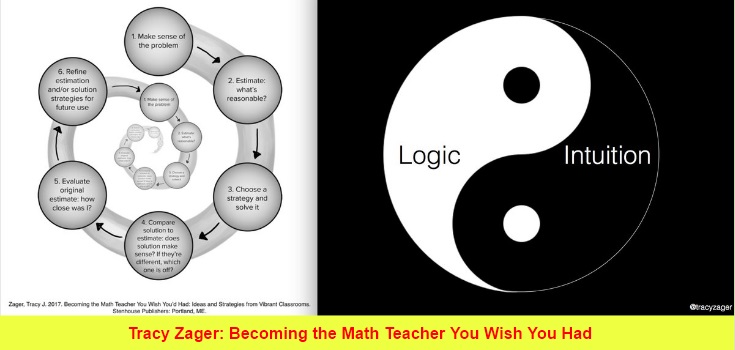
And of course, for me, two of the most powerful images on the topic have been shared by Tracy Zager (If you haven’t purchased her book: Becoming the Math Teacher You Wish You’d Had you need to!). The image on the left shows the process we go through when solving a problem. So much of what we want our students to do involves them making sense of things and considering their initial thoughts. The image on the right to me is even more powerful though. It shows just how important our intuition is, and how building our students’ intuition is key for them to build their logic! These two go hand-in-hand!
A few things to reflect on:
- What does estimation look like in your class? Is this a routine you do?
- Many of the ideas shared above might be more specific to the content you are learning. How do you help your students see the importance of estimation when you are learning new topics?
- When your class is estimating, how do you promote the range? Are some of your students still “guessing”? If so, how can you use the ideas of others in the room to help? How else can we improve here?
- Many of the ideas I shared above involved estimating without giving a number. These tasks often directly involve helping our students use their Spatial Reasoning. How are you helping your students develop their Spatial Reasoning?
- The students in our classrooms that are estimating all the time (even without them realizing it) do well in mathematics. Those that struggle often aren’t using their intuition. Why do some use their intuition more than others? What do WE have to do to help everyone use their intuition more often?
- Did you notice any relationships between the coloured images above? All the yellow ones involve… all the red ones are… I wonder which ones you gravitated toward?
As always, I encourage you to leave a message here or on Twitter (@markchubb3)!

















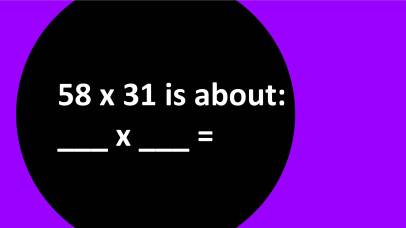





Couldn’t agree more. Just finished my inquiry project on this and I saw for myself just how empowering estimation can be for students. It reawakens their curiosity, their reasoning, and their motivation. Thanks for summing it up so clearly!
LikeLike
There is so much here, Mark. This is great. I’m so glad that you shared it again on Twitter otherwise it could’ve been some time until I had stumbled upon it. I have found that these are great entry points into lessons and open up dialogue for all learners right from the get-go. I have also found that some of my “weaker” students (I wish I could think of a better term) often estimate either unreasonably large or small estimations in comparison to most students, which to me indicates a disconnect between what the numbers actually represent and their own number sense. Thanks for sharing again!
LikeLike
Thanks John. I do hope that we are thinking of ways to help our students make connections and think about concepts before we have them plug in numbers and follow procedures. You are right about making this a priority for our students who might be currently struggling with the current topic… Getting us to estimate first is really helpful, especially for them!
Kind of like the forest for the trees analogy… some students need to take a step back and really think about the situation instead of trying to navigate in spaces where they can’t find their barrings.
Thanks John for the comment!
LikeLiked by 1 person
We asked our year 6 students to read your post and here were some of their comments:
“Estimating in my opinion is a higher order of thinking and makes you think harder about whatever your doing. When you have a set question and you know the formulas and strategies to work it out, it is easy. However when estimating, it makes you think about all the different possibilities of th question. Would it be closer to this? What determines this from that? All of these questions are asked when you estimate about something.” – Loni
“I agree this article because whilst reading this It made me realise how important estimating actually is. He listed some everyday that use estimation. Doing some of those things I never really realised that I was estimating. I estimate so often like when I bake or like when I am getting ready to go to the bus stop. I estimate when I should leave the house in order to get to the bus stop in time. Now thinking about it, estimating is a very important skill and I am very grateful to know how to estimate.” – Emma
LikeLike