A little more than a year ago now, Sarah Carter shared a set of Japanese puzzles called Zukei Puzzles (see her original post here or access her puzzles here). After having students try out the original package of 42 puzzles, and being really engaged in conversations about terms, definitions and properties of each of these shapes, I wanted to try to find more. Having students ask, “what’s a trapezoid again?” (moving beyond the understanding of the traditional red pattern block to a more robust understanding of a trapezoid) or debate about whether a rectangle is a parallelogram and whether a parallelogram is a rectangle is a great way to experience Geometry. However, after an exhaustive search on the internet resulting in no new puzzles, I decided to create my own samples.

Take a look at the following 3 links for your own copies of Zukie puzzles:
Copy of Sarah’s translated Zukei puzzles
Extension puzzles #1
Extension puzzles #2
Advanced Zukei Puzzles #3
I’d be happy to create more of these, but first I’d like to know what definitions might need more exploring with your students. Any ideas would be greatly appreciated!
How to complete a Zukei puzzle:
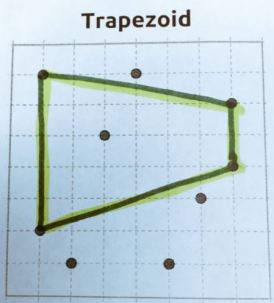
Each puzzle is made up of several dots. Some of these dots will be used as verticies of the shape named above the puzzle. For example, the image below shows a trapezoid made of 4 of the dots. The remaining dots are inconsequential to the puzzle, essentially they are used as distractors.
If you enjoyed these puzzles, I recommend taking a look at Skyscraper puzzles for you to try as well.
Thanks so much for making more of these. Unfortunately I cannot remember the rules of the puzzle. Is it just to make the required shape connecting any of the dots or must there be a certain number of dots inside/outside the puzzle or ??
I’d love even more – will definitely try these with students!
Thanks in advance for letting me know.
Karen
LikeLiked by 1 person
I’ll add some rules. Thanks for the feedback.
LikeLike
Did you know there is an app with similar puzzles? It is called “Pythagorea”. I think you’d like it!
LikeLiked by 2 people
I’ll definitely take a look.
LikeLike
Excited to check out that app! Working on a set of puzzles for elementary kids and thinking about making more with some of the more basic shapes.
LikeLike
My students LOVE these! Thank you for sharing your version.
LikeLike
Thank you! I love your skyscraper puzzles, too!
LikeLike
I gave my third graders just the puzzles that addressed quadrilaterals and it was eye opening as far as them understanding the attributes…
Embarrassed to ask… is there an answer key? I am stumped on the parallelogram puzzle (2nd row on the right) in extension puzzles #2…
LikeLike
I have not made an answer key (on purpose). I’d rather that we have more people continuing to talk about mathematics than just giving out answers. However…. if you are stuck on this one problem…. you might notice 4 dots in the middle of the page, toward the bottom…. where two of the sides are positioned perpendicular to the bottom of the page. There will be 2 unused dots to the left of this shape… 2 unused dots to the right… and 2 unused dots above it.
Hopefully this helps:)
LikeLike
Ooooooohhhh…. found it 🙂 Thanks!
LikeLike
excellent idea. the pupils enjoyed it.
LikeLike
I love these puzzles! Thank you for making some more 🙂
I also LOVE your skyscraper puzzles. I was teaching a 6th grade elective this spring and used them with the class. After reading your post on it in preparation I decided to make a Slides ppt for them. They wanted to know who you were so I added your Twitter pic to the first slide. Here it is if you’d like to use it too! https://docs.google.com/presentation/d/1rNNqEVUlHARcmpMd2sN2KnNxsV4qeevvAxgAEVgrTX8
LikeLiked by 2 people
Thanks for sharing your slideshow. Excited that you are sharing these with others.
LikeLike
These are fun, and great! What I’d *really* like to see (no obligation, of course) are puzzles where the puzzler is to find multiple figures on these dots. For example, “Find a square, two rhombuses, and four isosceles triangles”. That would allow for several correct answers per puzzle, and students would then piece together the fact that there would be four isosceles right triangles for each square…
LikeLiked by 1 person
Could I make your extension and advanced puzzles into a Desmos Activity Builder? I made one for Sarah’s puzzles. https://teacher.desmos.com/activitybuilder/custom/585b4540f24bc103154b8f3a
LikeLiked by 1 person
Go for it. I’d love to see the final product.
LikeLike
> The remaining dots are inconsequential to the puzzle, essentially they are used as distractors.
Not so.
There are a ton of trapezoids in there, https://i.imgur.com/vOZxqu4.jpg
LikeLike
Thanks for this Jacob. For these puzzles I have used the definition of a trapezoid which states it is a quadrilateral with 1 pair of parallel sides (meaning exactly one pair, not at least 1 pair). However, if your definition differs, I would be happy you found other answers. I am quite happy that you’ve found multiple possibles here…but for each possible answer the other points are unused. Hope that makes sense. Thanks for the pictures.
LikeLike
The standard definition of trapezoid accepted by essentially everyone is a convex quadrilateral with at least one pair of parallel sides. https://en.wikipedia.org/wiki/Trapezoid
In this particular puzzle, 3 of the trapezoids are also parallelograms (2 pairs of parallel sides), 1 of the trapezoids is isoceles, and 5 are scalene. Among the scalene trapezoids, 1 is a right trapezoid, 2 are acute, and 2 are obtuse.
There are 6 in total matching your definition which excludes parallelograms. Whoops, I accidentally highlighted the same parallelogram twice in my images. So only 9 total by the standard definition, assuming I didn’t miss any.
LikeLike
Personally, I’m much more interested in this conversation than students all finding the same answers. I have other specific examples of exactly what you’re doing here. Take a look:
https://buildingmathematicians.wordpress.com/2017/11/09/how-many-do-you-seepart-1/
LikeLike
I count 47 trapezoids in your other exercise, and 14 triangles. The other shapes aren’t too interesting:
LikeLike
Hmmm… and I thought the hexagons might be quite interesting?
LikeLike
Ah that’s true. If you allow arbitrary hexagons there are a whole lot. Let me try to count them for you, give me a minute.
LikeLike
Actually I missed a few there. Looking more carefully, I count 10 total, including at least three through each dot.
LikeLike
Have you ever seen Feuerstein’s Instrumental Enrichment “organisation of dots” tool? Check it out.
LikeLike
We have searched for hours but cannot find the second parallelogram in the Zukei Puzzles #3 for the puzzle 2 Parallelograms. Please help.
LikeLike
Both of the parallelograms here have a bottom parallel to the bottom of the page. The 2 parallelograms share a common point.
LikeLike
Thank you, I found it!
LikeLike
I’m so excited I found your page! I will definitely use them next year! I’m not sure if you are still looking for ideas of shapes our students struggle with… but for my 5th graders it’s the hierarchy concept. Ex) the idea that any quadrilateral with 2 pairs parallel lines can be a parallelogram, including ones we’d usually call squares, rectangles and rhombi. So I’d love to see ones where maybe they are looking for a rectangle, and the only rectangle possibility is a square. You may have some in there already – I definitely haven’t tried them all yet! Thanks for all the puzzles you do have! They are great!
LikeLike
For the challenge puzzles (#3) I found the middle row but backwards. The left puzzle I found 2 rectangles and the right puzzle I found 3 parallelograms. Does the left also have 3 parallelograms?
LikeLike
Very interesting subject , thankyou for posting.
LikeLike