“Number Boxes”

A few weeks ago I was introduced to Jenna Laib‘s game “Number Boxes” and was very interested in using it as a dynamic game to help students learn a variety of new content — Jenna’s blog explaining the game can be found here: “One of My Favorite Games: Number Boxes“.

Basically the game involves students rolling dice (or spinning a spinner / drawing a card) to generate a random number and placing that number in one of their empty number boxes one-at-a-time. The game can progress in a variety of ways:

Rolling 1 number at a time, create the largest number you can.

Rolling one number at a time, create 2 numbers that will add to the largest number.

Rolling one number at a time, create an expression that is as close to 2000 as possible.

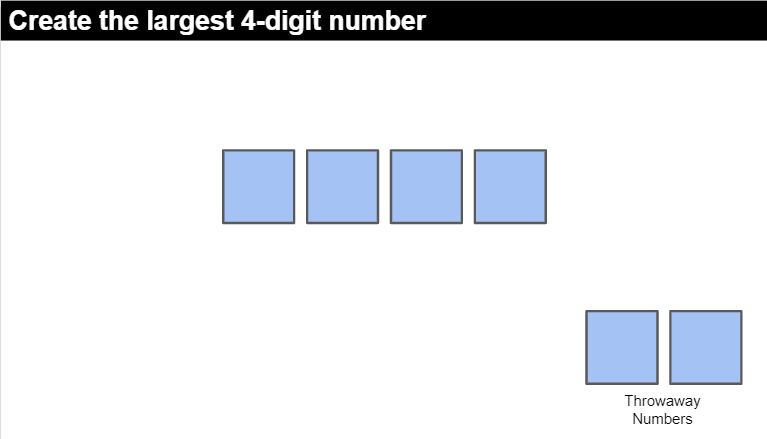
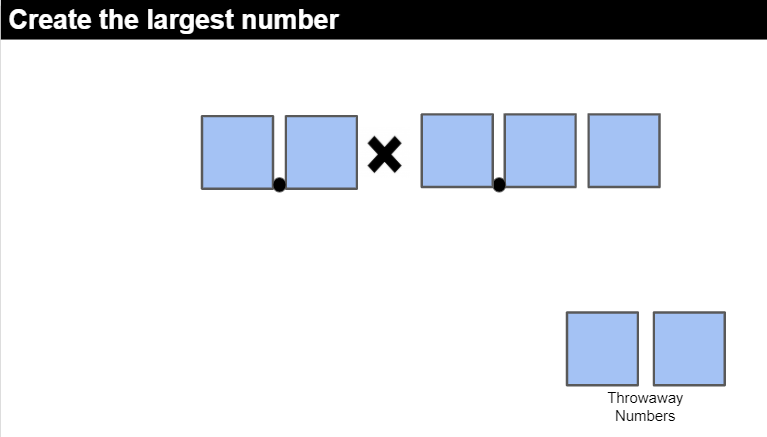
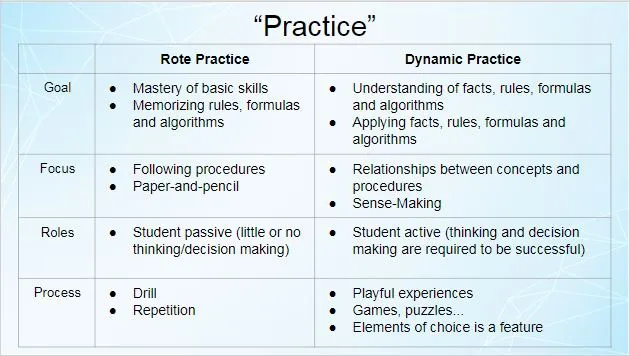
As you can see, the game is quite adaptive to the sizes of numbers and concepts your students are comfortable with. As students roll/spin/draw a number, they have to place it on the board. What makes this tricky is not knowing what future numbers will be. In the board above, you can see that there is also a “Throwaway” box that students can use if they do not like one of the numbers rolled/spun/drawn. This game is an excellent example of a “Dynamic Game” or “Dynamic Practice” as students are following the ideals on the right side of the chart below:

Originally published here

Blow is a gallery of some possible adaptations of this game or linked here is a slideshow

• 

• 

• 

• 

• 

• 

• 

• 

Metric Conversions

I however, wanted to use Jenna’s game to help students practice a concept they often have difficulty with – Metric Conversions. Once students have had many opportunities to estimate and measure various distances, capacities, and masses, they should be able to start making connections between all of the units. I suggest a good balance between using problems that help students make sense of the relationships between the units, and opportunities to practice conversions on their own. However, instead of randomly generated worksheets or other rote practice, I think Jenna’s game could work perfectly. Take a look at some examples:

Rolling one number at a time, find the largest total distance possible

Rolling one number at a time, find the largest total mass possible

Rolling one number at a time, find the largest possible distance

Rolling one number at a time, how close to 5km can you get?

Reflection

It is important to offer tasks that allow students to make choices and decisions like the ones offered in this game. Learning needs to be more than handing out assignments, and collecting work… Learning takes time! Students need more time to explore, see what works, have peers challenge each others’ thinking, make important connections… Hopefully you can see these opportunities in this task.

Final Thoughts:

• If you play one of these games, or your own version, will you first offer a simplified version so your students get familiar with the game, or will you dive into the content you want to teach?
• Would you prefer your students to play this game as a class or with a group, a partner, or independently?
• How will you build in conversations with students so they discuss which numbers they think should be the highest / lowest numbers? How will you offer time for these strategic discussions?
• Should we adapt these to continually offer more challenge and deeper learning, or offer more opportunities to play the same game board? How will we know when to adapt and change?
• What does “practice” look like in your classroom?  Does it involve thinking or decisions?  Would it be more engaging for your students to make practice involve more thinking?
• How does this game relate to the topic of “engagement”?  Is engagement about making tasks more fun or about making tasks require more thought?  Which view of engagement do you and your students subscribe to?
• How have your students experienced measurement concepts like these? Are they learning procedural rules or are they thinking about the actual sizes of numbers / sizes of the units involved?
• As the teacher, what will you be doing when students are playing? How might listening to student thinking help you learn more about your students? (See: Noticing and Wondering: A powerful tool for assessment)

I’d love to continue the conversation about “practicing” mathematics.  Leave a comment here or on Twitter @MarkChubb3

How Big is “Big”?

In the last few weeks I have asked several groups of teachers to indicate where 1 billion would go on this number line:

It has been really interesting to me that many have placed the 1 billion mark in a variety of areas and have had a variety of reasons why.  Many have attempted to use their understanding of place value digits  (there are 12 zeros in 1 trillion and only 9 zeros in 1 billion, so 1 billion should be 3/4 of the way toward a trillion) or their knowledge of prefixes to help (million, billion, trillion… so it must be 2/3 the way along the line). Others thought about how many billions are in a trillion asking themselves, “Is their one-hundred or one-thousand billions in a trillion?” Using this strategy, everyone picked a spot toward the left, but some much closer to zero than others.

Others did something interesting though. They started placing other numbers on the number line to help them make sense of the question. Often placing 500 billion in the middle, then 250 billion at the 1/4 mark and so on until they realized just how close to 0 a billion is when we are considering 1 trillion.

What’s the point?

Really big numbers, and really small numbers (decimal numbers), are difficult to conceptualize!  They are hard to imagine their size!  Think about this:

How long is 1 million seconds?  Without doing ANY calculations would you guess the answer is several minutes, hours, days, weeks, months, years, decades, centuries…?  Can you even imagine a million seconds without calculating anything?

How about 1 billion seconds?  Or 1 trillion seconds?

I bet you’ve started trying to calculate right!  That’s because these numbers are so abstract for us that we can’t imagine them.

Because of this little experiment, I am left wondering three things:

1. What numbers can/can’t the students in our classrooms conceptualize?
2. What practices do we do that gets kids to think about digits more than magnitude?
3. What practices could/should we be including that helps our students make these connections?

---

What numbers can/can’t the students in our classrooms conceptualize?

Before we start working with operations of any given size, I think we need to spend time making sure our students can visualize and estimate the size of the number.  Working with numbers we can’t imagine doesn’t seem productive for our young students!  In our rush to move our kids into more “complicated” mathematics, we often move too quickly through numbers to include numbers that are too abstract for our students!  We think that if a student can accurately carry out a procedure that they understand the numbers they are working with. However, I’m sure we have all seen many students who produce answers that are completely unreasonable without them noticing. Is this carelessness, or is it a lack of understanding of the magnitude of the numbers involved?  Or possibly that our students aren’t visualizing the size of and relationship between the numbers???

---

What practices do we do that gets kids to think about digits more than magnitude?

The other day, Jamie Garner shared her frustration on Twitter:

Think about the question from the textbook for a second. Students trying to think about 342 pencils (not sure why they would want that many) should be considering a strategy that makes sense. For example, if you had 342 pencils how many boxes of 10 would that be?  Thinking this way, student should answer 34 or 34.2, or maybe 35 boxes (if you wanted to purchase enough boxes).  However, the teacher’s edition tells us that none of these are the right answer. Take a look:

If our students attempt to make sense of the problem, they will be completely wrong!  In fact, many students will likely answer 4 because they’ve been trained not to think at all about the mathematics, and instead focus their attention on what they think the text wants them to do.

This is one of MANY cases where elementary mathematics focuses on digits over understanding magnitude or relative size.  Here are a few others:

These, along with pretty much any standard algorithm (see Christopher Danielson’s post: Standard Algorithms Unteach Place Value) tell our kids to stop thinking about what makes sense, and instead focus on steps that help kids get an answer without understanding.

---

What practices could/should we be including that helps our students make these connections?

If we want our students to understand numbers, and their relative size… if we want to help our students develop a conceptual understanding of operations… if we want our students make sense of the math they are learning… then we need to:

• Use contexts that make sense to our students (not pseudo-contexts like the pencil question above).
• Provide plenty of experiences where students are making sense of numbers visually.  When we allow our students to access their Spatial Reasoning we are allowing them to see the relationship between numbers and help them make connections between concepts.
• Provide plenty of experiences estimating with numbers

Below are 2 activities taken from Van de Walle’s Student Centered Mathematics.  Think about how you could adapt these to work with numbers your students are starting to explore (really big or really small numbers).

---

A few questions for you to reflect on:

• How might you see how well your students understand the numbers that are really large or really small?
• How are you helping your students develop reasonableness when working with numbers?
• What visuals are you using in your class that help your students visualize the numbers you are working with?
• What practices do you use regularly that help with any of the 3 above?

---

P.S. Here are the answers to the seconds problem I posted earlier: