Taking an Equity Stance in Math Class

Ask any teacher anywhere what some of the most pressing challenges are that they face as a teacher and likely you will hear examples of how difficult it can be to meet the various needs within a classroom. When conversations on the topic arise, there are often discussions from one of two extremes:

One one side you might hear about reasons why a teacher might believe that it is best to make sure that every student be expected to learn the same things. These beliefs often lead to practices where everyone receives the same instruction, followed by individual assistance for students who were not able to follow classroom instructions. Equity here is believed to be related to equal outcomes.

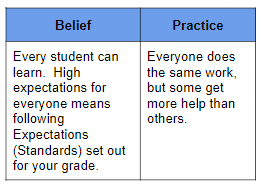
On the other hand, some teachers might believe that it isn’t possible to expect every student to learn the same things at the same time. Their beliefs lead them to focus more attention on determining readiness and offering different groups of students different learning opportunities. Equity here is viewed as meeting each child’s unique need.

While I understand each of these points of view, part of the issue between these two views is the overall view of what mathematics is. If mathematics is seen as a set of linearly learned skills, where each skill is boiled down to a list of subskills, each learned in a specific sequence, it is difficult to imagine anything else. However, when mathematics is seen through the lens of rich connections, we might start to see students’ development of these connections as what can drive our decisions.

One way to think of a person’s understanding of mathematics is that it exists along a continuum. At one end is a rich set of connections. At the other end of the continuum, ideas are isolated or viewed as disconnected bits of information. A sound understanding of mathematics is one that sees the connections within mathematics and between mathematics and the world.

TIPS4RM: Developing Mathematical Literacy, 2005

The two views mentioned above do not account for a view of mathematics where connections between concepts is a focus. Instead of seeing the issue as simply whether or not we want a classroom of students to be doing the same things or if we should be providing some students with different things, we should also consider what is actually being learned by the students. Below you can see a matrix showing four different examples of how we could tackle the same concept in a classroom:

Same / Different Learning? Same / Different Tasks?

Same Tasks, Same Learning: The teacher offers everyone the same task, expects everyone to be able to follow the same procedures and might offer explicit help to specific students that aren’t following accordingly.

Different Tasks, Same Learning: While everyone is learning the same thing, the teacher offers some groups easier work and other groups more advanced work based on readiness.

Different Tasks, Different Learning: Based on diagnostic assessments, students are placed into groups based on what they need to continue learning. Some groups might be learning different materials within the same class.

Same Tasks, Different Learning: Every student is provided the same task, but there is variance in how and what is being learned.

For the readers here, I encourage you to think about which of the above models might you have experienced as a student, and which you might think would be best for your students.

Taking an Equity Stance

So, what does any of this have to do with equity? In my experience, a lot! Taking an equity stance means that we both believe that every student can achieve, and understand that every student might need different things from us. Keeping equity in mind requires us to analyze who has access to rich mathematical experiences and whose experiences are narrowed or reduced to lower-level skills (Access), whose ideas contribute to the group’s development of mathematical understanding and whose are not heard (Agency and Authority), who identifies with mathematics and who does not (Identity)… Without considering our beliefs and practices, we will never be able to notice which students are being underserviced, which structures promote some groups over others, or see which practices lead to the “Matthew Effect“.

How do we aim for Equity?

When thinking about how we aim for equity in mathematics, there seems to be 2 key tenets that help point us in the right direction:

• Expand WHO is considered a math student
• Expand WHAT is accepted as mathematics

The question is not whether all students can succeed in mathematics but whether the adults organizing mathematics learning opportunities can alter traditional beliefs and practices to promote success for all.

Principles to Action – NCTM (p.61)

WHO is considered a math person?

Teachers who come to recognize that some students identify with mathematics (and others do not) aim to promote tasks that allow more students to engage in mathematical reasoning via problems/tasks that are easily accessible (low-floor, high-ceiling tasks). If our students are going to see themselves as budding mathematicians, then we need to allow more opportunities for students to share their emerging ideas first!

Dr. Christine Suurtamm does a great job of articulating what this could look like in practice:

Dr. Christine Suurtamm

Students need to see themselves in the work they are doing. This includes knowing that mathematics is not created for and used by only some people (race/gender…), nor is it only useful for potential futures of some of our students, but is actually used by all of us RIGHT NOW. If we want to make sure our students see themselves as mathematicians, OUR STUDENTS need to be doing more of the thinking, they need to be part of the process of learning, not simply showing that they have mastered procedures.

Reflecting on WHO believes they are a math person might help us reflect on what messages our students have received over the years. If you haven’t already read about the “Matthew Effect“, I recommend that this might be a great place to help you reflect.

WHAT Counts as “Mathematics”?

To some, mathematics is a very narrow subject. Calculating (adding, subtracting, multiplying, dividing), converting (equivalent fractions), and carrying out other procedures accurately by using the requisite steps… Procedures dominate some textbooks and online practice sites and for some, this narrow vision of mathematics is where some students begin to struggle. However, if we are aiming for equity then we need to allow more opportunities for our students to show us what ARE good at.

One way to expand what counts as mathematics is for us to reflect on how much time we spend on each strand of mathematics (Patterning, Number Sense, Geometry, Measurement, Data Management). Analyzing how much time we spend on each of these strands, and specifically when in the year we might teach these concepts might help us reflect on what messages our students hear when they consider what counts as mathematics. For example, schools in my area typically start with several weeks of patterning because it can be experienced physically (manipulatives) and visually (visual patterns, graphing…), followed by several weeks of Geometry. These moves were strategic, because it allows our students more opportunities to talk, more opportunities to solve problems, more opportunities for our students to use visual/ spatial reasoning and more students to start their year with successes!

Expanding what mathematics means is much more than strands or concepts though. A focus on concrete and visual representations (not solely abstract symbolic representations) can be a path to expand what counts as mathematics. Allowing students to show their strategies, and accepting student strategies as part of the learning process means that preformal representations and strategies can be compared and learned from.

Spatial puzzles and games allow students to think mathematically in ways that differ from typical assignments. A story I often tell is of this young student who had never liked mathematics, and often struggled with mathematics. Here you can see her attempting to solve a difficult puzzle that one of her classmates created. Every child deserves to experience what this student experienced – productive struggle and success. Take a look:

Considerations

If we are aiming for equity in our own personal practices, we need to be aware of our own biases, our own patterns. This isn’t easy! It might mean noticing how we talk about race or gender or socio-economic groups and what our expectations are for each. It might mean reflecting on words we use to discuss students who might currently be struggling to learn mathematics or who are identified learners and what our expectations are of these students. Again, learning more about the Matthew Effect is where I would recommend you start. Planning with providing greater access for students to learn mathematics (same tasks/different learning – spatializing mathematics) is likely a first concrete step we can take.

I want to leave you with a few reflective questions:

• How do you see the Same/Different Learning – Same/Different Tasks chart relating to equity? Which quadrant would you like provide for your students to be engaged with more frequently? What barriers are standing in the way?
• We need to be aware that when schools group students by ability or assign different tasks to different students, those that are relegated to lower groups/tasks often receive lower level of cognitive demand tasks, which often puts them at a further disadvantage than their peers. How do you combat these inequities in your classroom?
• Providing students with rich tasks and access to rich problems isn’t enough. We also need to be noticing our students’ thinking so we know how to respond to our students individually and as a group. This isn’t easy! How do you pay attention to their thinking? What structures do you have in place to listen to students and respond accordingly?
• How do you monitor your students’ interests and thoughts about mathematics in general, or about specific concepts?
• How are you aiming to minimize the Matthew Effect and reduce inequities in your room?

As always, I’d love to hear your thoughts.  Leave a reply here on Twitter (@MarkChubb3)

An Example of Teaching THROUGH problem solving?

Many math resources attempt to share the difference between teaching FOR problem solving and teaching THROUGH problem solving. Cathy Seeley refers to teaching THROUGH problem solving as “Upside-Down Teaching” which is the opposite of a “gradual release of responsibility” model:

And instead calls for us to flip how our students learn to a more active model:

So, instead of starting a unit on Geometry with naming shapes or developing definitions together, we decided to start with a little problem:

Create as many polygons as possible using exactly 2 pattern block pieces. Sort your polygons by how many sides they have.

As students started placing pattern block pieces together, all kinds of questions started emerging (questions we took note of to bring to the whole group in a few minutes):

What is this shape called? It has 6 sides, so is it a hexagon?

This shape has 12 sides. Am I allowed to do this?

Are these the same shapes or different? Do I have to line up the sides or can I place a shape in the middle like I did here (on the right)?

By the end of a period, students had worked through the definitions of what a polygon is (and isn’t), the difference between concave and convex polygons, defined the term “regular polygon” (which was not what they had been calling “regular” before), and were able to name and create triangles, quadrilaterals, pentagons, hexagons, heptagons, octagons, nonagons, decagons and undecagons. Recognizing a variety of possible ways a shape can look was very helpful for our students who might have experienced shapes more traditionally in the past.

One group compiled their polygons together (with one minor error):

Instead of starting with experiences where students accumulate knowledge (writing out definitions, taking a note, direct instruction), an upside down approach aims to start with students’ ideas. This way we would know which conversations to have with our students, and so our students are actively engaged in the process of learning.

I want to leave you with a few reflective questions:

• Why might it benefit students to start with a problem instead of starting with the teachers’ ideas?
• Why might it benefit teachers to listen to students’ thinking before instruction has occurred?
• What does it mean to effectively monitor students as they are thinking / working? (See This POST for examples)
• Can all mathematics topics begin with tasks that help our students make connections between what they already know, and what they are learning? Can you think of a topic that can not be experienced this way?
• The final stage in the You-We-I model is where the teacher helps make specific learning explicit for their students. How do you find time to consolidate a task like this? How do you know what to share? (See This POST for an example)
• How might this form of teaching relate to how we view assessment? (See This POST)
• How might this form of teaching relate to how we view differentiated instruction? (See This POST)
• How do you find problems that ask students to actively think before any instruction has occurred? (See This POST for examples)

I’d love to continue the conversation.  Feel free to write a response, or send me a message on Twitter ( @markchubb3 ).

Rushing for Interventions

I see students working in groups all the time…  Students working collaboratively in pairs or small groups having rich discussions as they sort shapes by specific properties, students identifying and extending their partner’s visual patterns, students playing games aimed at improving their procedural fluency, students cooperating to make sense of a low-floor/high-ceiling problem…..

When we see students actively engaged in rich mathematics activities, working collaboratively, it provides opportunities for teachers to effectively monitor student learning (notice students’ thinking, provide opportunities for rich questioning, and lead to important feedback and next steps…) and prepare the teacher for the lesson close.  Classrooms that engage in these types of cooperative learning opportunities see students actively engaged in their learning.  And more specifically, we see students who show Agency, Ownership and Identity in their mathematics learning (See TruMath‘s description on page 10).

---

On the other hand, some classrooms might be pushing for a different vision of what groups can look like in a mathematics classroom.  One where a teachers’ role is to continually diagnose students’ weaknesses, then place students into ability groups based on their deficits, then provide specific learning for each of these groups.  To be honest, I understand the concept of small groups that are formed for this purpose, but I think that many teachers might be rushing for these interventions too quickly.

First, let’s understand that small group interventions have come from the RTI (Response to Intervention) model.  Below is a graphic created by Karen Karp shared in Van de Walle’s Teaching Student Centered Mathematics to help explain RTI:

Response to Intervention – Teaching Student Centered Mathematics

As you can see, given a high quality mathematics program, 80-90% of students can learn successfully given the same learning experiences as everyone.  However, 5-10% of students (which likely are not always the same students) might struggle with a given topic and might need additional small-group interventions.  And an additional 1-5% might need might need even more specialized interventions at the individual level.

The RTI model assumes that we, as a group, have had several different learning experiences over several days before Tier 2 (or Tier 3) approaches are used.  This sounds much healthier than a model of instruction where students are tested on day one, and placed into fix-up groups based on their deficits, or a classroom where students are placed into homogeneous groupings that persist for extended periods of time.

---

Principles to Action (NCTM) suggests that what I’m talking about here is actually an equity issue!

Principles to Action

We know that students who are placed into ability groups for extended periods of time come to have their mathematical identity fixed because of how they were placed.  That is, in an attempt to help our students learn, we might be damaging their self perceptions, and therefore, their long-term educational outcomes.

---

Tier 1 Instruction

While I completely agree that we need to be giving attention to students who might be struggling with mathematics, I believe the first thing we need to consider is what Tier 1 instruction looks like that is aimed at making learning accessible to everyone.  Tier 1 instruction can’t simply be direct instruction lessons and whole group learning.  To make learning mathematics more accessible to a wider range of students, we need to include more low-floor/high-ceiling tasks, continue to help our students spatalize the concepts they are learning, as well as have a better understanding of developmental progressions so we are able to effectively monitor student learning so we can both know the experiences our students will need to be successful and how we should be responding to their thinking.  Let’s not underestimate how many of our students suffer from an “experience gap”, not an “achievement gap”!

If you are interested in learning more about what Tier 1 instruction can look like as a way to support a wider range of students, please take a look at one of the following:

•  How do we meet the needs of so many unique students in a mixed-ability classroom?
• Differentiated Instruction: comparing 2 subjects
• Differentiating Mathematics Instruction

---

Tier 2 Instruction

Tier 2 instruction is important.  It allows us to give additional opportunities for students to learn the things they have been learning over the past few days/weeks in a small group.  Learning in a small group with students who are currently struggling with the content they are learning can give us opportunities to better know our students’ thinking.  However, I believe some might be jumping past Tier 1 instruction (in part or completely) in an attempt to make sure that we are intervening. To be honest, this doesn’t make instructional sense to me! If we care about our content, and care about our students’ relationship with mathematics, this might be the wrong first move.

So, let’s make sure that Tier 2 instruction is:

• Provided after several learning experiences for our students
• Flexibly created, and easily changed based on the content being learned at the time
• Focused on student strengths and areas of need, not just weaknesses
• Aimed at honoring students’ agency, ownership and identity as mathematicians
• Temporary!

If you are interested in learning more about what Tier 2 interventions can look like take a look at one of the following:

• RTI for Adults
• Targeted Instruction
• Continuing to get better together

---

Instead of seeing mathematics as being learned every day as an approach to intervene, let’s continue to learn more about what Tier 1 instruction can look like!  Or maybe you need to hear it from John Hattie:

Or from Jo Boaler:

---

Final Thoughts

If you are currently in a school that uses small group instruction in mathematics, I would suggest that you reflect on a few things:

• How do your students see themselves as mathematicians?  How might the topics of Agency, Authority and Identity relate to small group instruction?
• What fixed mindset messaging do teachers in your building share “high kids”, “level 2 students”, “she’s one of my low students”….?  What fixed mindset messages might your students be hearing?
• When in a learning cycle do you employ small groups?  Every day?  After several days of learning a concept?
• How flexible are your groups?  Are they based on a wholistic leveling of your students, or based specifically on the concept they are learning this week?
• How much time do these small groups receive?  Is it beyond regular instructional timelines, or do these groups form your Tier 1 instructional time?
• If Karp/Van de Walle suggests that 80-90% of students can be successful in Tier 1, how does this match what you are seeing?  Is there a need to learn more about how Tier 1 approaches can meet the needs of this many students?
• What are the rest of your students doing when you are working with a small group?  Is it as mathematically rich as the few you’re working with in front of you?
• Do you believe that all of your students are capable to learn mathematics and to think mathematically?

I’d love to continue the conversation.  Write a response, or send me a message on Twitter ( @markchubb3 ).

Targeted Instruction

The other day I was asked about my opinion about something called entrance slips. Curious about their thoughts first, I asked a few question that helped me understand what they meant by entrance slips, what they would be used for, and how they might believe they would be helpful. The response made me a little worried. Basically, the idea was to give something to students at the beginning of class to determine gaps, then place students into groups based on student “needs”.  I’ll share my issues with this in a moment…  Once I had figured out how they planned on using them, I asked what the different groups would look like.  Specifically, I asked what students in each group would be learning. They explained that the plan was to give an entrance slip at the beginning of a Geometry unit. The first few questions on this entrance slip would involve naming shapes and the next few about identifying isolated properties of shapes. Those who couldn’t name shapes were to be placed into a group that learns about naming shapes, those who could name shapes but didn’t know all of the properties were to go into a second group, and those who did well on both sections would be ready to do activities involving sorting shapes.  In our discussion I continually heard the phrase “Differentiated Instruction”, however, their description of Differentiated Instruction definitely did not match my understanding (I’ve written about that here). What was being discussed here with regards to using entrance slips I would call “Individualized Instruction”.  The difference between the two terms is more than a semantic issue, it gets to the heart of how we believe learning happens, what our roles are in planning and assessing, and ultimately who will be successful.  To be clear, Differentiated Instruction involves students achieving the same expectations/standards via different processes, content and/or product, while individualized or targeted instruction is about expecting different things from different students.

---

Issues with Individualized / Targeted Instruction

Individualized or targeted instruction makes sense in a lot of ways.  The idea is to figure out what a student’s needs are, then provide opportunities for them to get better in this area.  In practice, however, what often happens is that we end up setting different learning paths for different students which actually creates more inequities than it helps close gaps.  In my experience, having different students learning different things might be helpful to those who are being challenged, but does a significant disservice to those who are deemed “not ready” to learn what others are learning.  For example, in the 3 pathways shared above, it was suggested that the class be split into 3 groups; one working on defining terms, one learning about properties of shapes and the last group would spend time sorting shapes in various ways.  If we thought of this in terms of development, each group of students would be set on a completely different path.  Those working on developing “recognition” tasks (See Van Hiele’s Model below) would be working on low-level tasks.  Instead of providing experiences that might help them make sense of Geometric relationships, they would be stuck working on tasks that focus on memory without meaning.

When we aim to find specific tasks for specific students, we assume that students are not capable of learning things others are learning.  This creates low expectations for our students!  Van de Walle says it best in his book Teaching Student Centered Mathematics:

Determining how to place students in groups is an important decision.  Avoid continually grouping by ability.  This kind of grouping, although well-intentioned, perpetuates low levels of learning and actually increases the gap between more and less dependent students.  

Targeted instruction might make sense on paper, but there are several potential flaws:

• Students enter into tracks that do not actually reflect their ability.  There is plenty of research showing that significant percentages of students are placed in the wrong grouping by their teachers.  Whether they have used some kind of test or not, groupings are regularly flawed in predicting what students are potentially ready for.
• Pre-determining who is ready for what learning typically results in ability grouping, which is probably the strongest fixed mindset message a school can send students.  Giving an entrance ticket that determines certain students can’t engage in the learning others are doing tells students who is good at math, and who isn’t.  Our students are exquisitely keen at noticing who we believe can be successful, which shapes their own beliefs about themselves.
• The work given to those in lower groups is typically less cognitively demanding and results in minimal learning.  The intent to “fill gaps” or “catch kids up” ironically increases the gap between struggling students and more independent learners.  Numerous studies have confirmed what Hoffer (1992) found: “Comparing the achievement growth of non-grouped students and high- and low-group students shows that high-group placement generally has a weak positive effect while low-group placement has a stronger negative effect. Ability grouping thus appears to benefit advanced students, to harm slower students.“

---

 

The original conversation I had about Entrance Tickets illustrated a common issue we have.  We notice that there are students in our rooms who come into class in very different places in their understanding of a given topic.  We want to make sure that we provide things that our students will be successful with… However, this individualization of instruction does the exact opposite of what differentiated instruction intends to do.  Differentiated instruction in a mathematics class is realized when we provide experiences for our students where everyone is learning what they need to learn and can demonstrate this learning in different ways.  The assumption, however, is that WE are the ones that should be determining who is learning what and how much.  This just doesn’t make sense to me!  Instead of using entrance tickets, we ended up deciding to use this problem from Van de Walle so we could reach students no matter where they were in their understanding.  Instead of a test to determine who is allowed to learn what, we allowed every student to learn!  This needs to be a focus!

If we are ever going to help all of our students learn mathematics and believe that they are capable of thinking mathematically, then we need to provide learning experiences that ALL of our students can participate in.  These experiences need to:

• Have multiple entry points for students to access the mathematics
• Provide challenge for all students (be Problem-Based)
• Allow students to actively make sense of the mathematics through mathematical reasoning
• Allow students opportunities to students to express their understanding in different ways or reach an understanding via different strategies

Let’s avoid doing things that narrow our students’ learning like using entrance tickets to target instruction!  Let’s commit to a view of differentiated instruction where our students are the ones who are differentiating themselves (because the tasks allowed for opportunities to do things differently)!  Let’s continue to get better at leveraging students’ thinking in our classrooms to help those who are struggling!  Let’s believe that all of our students can learn!  

---

I want to leave you with a few reflective questions:

• Why might conversations about entrance tickets and other ways to determine students ability be more common today?  We need to use our students’ thinking to guide our instruction, but other than entrance cards, how can we do this in ways that actually help those who are struggling?
• Is a push for data-driven instruction fueling this type of decision making?  If so, who is asking for the data?  Are there other sources of data that you can be gathering that are healthier for you and your students?
• If you’ve ever used entrance tickets or diagnostics, followed by ability groups, how did those on the bottom group feel?  Do you see the same students regularly in the bottom group?  Do you see a widening gap between those dependent on you and those who are more independent?
• Where do you look for learning experiences that offer this kind of differentiated instruction?  Is it working for the students in your class that are struggling?

---

I encourage you to continue to think about what it means to Differentiate your Instruction.  Here are a few pieces that might help:

•  How do we meet the needs of so many unique students in a mixed-ability classroom?
• Differentiated Instruction: comparing 2 subjects
• RTI for Adults
• John Hattie discussing Ability Grouping
• Differentiating Mathematics Instruction

I’d love to continue the conversation.  Write a response, or send me a message on Twitter ( @markchubb3 ).

Differentiated Instruction: comparing 2 subjects

I’ve been thinking a lot about how to meet the various needs of students in our classrooms lately.  If we think about it, we are REALLY good at differentiated instruction in subjects like writing, yet, we struggle to do differentiated instruction well in subjects like math.  Why is this???

In writing class, everyone seems to have an entry point.  The teacher puts a prompt up on the board and everyone writes.  Because the prompt is open, every student has something to write about, yet the writing of every student looks completely different. That is, the product, the process and/or the content differs for each student to some degree.

Teachers who are comfortable teaching students how to write know that they start with having students write something, then they provide feedback or other opportunities for them to improve upon.  From noticing what students do in their writing, teachers can either ask students to fix or improve upon pieces of their work, or they can ask the class to work on specific skills, or ask students to write something new the next day because of what they have learned.  Either way the teacher uses what they noticed from the writing sample and asks students to use what they learned and improve upon it!

---

In Math class, however, many teachers don’t take the same approach to learning.  Some tell every student exactly what to do, how to do it, and share exactly what the finished product should look like.  OR… in the name of differentiated instruction, some teachers split their class into different groups, those that are excelling, those that are on track, and those that need remediation.  To them, differentiated instruction is about ability grouping – giving everyone different things.  The two teachers’ thinking above are very different aren’t they!

Imagine these practices in writing class again.  Teacher 1 (everyone does the exact same thing, the exact same way) would show students how to write a journal (let’s say), explain about the topic sentence, state the number of sentences needed per paragraph, walk every student through every step.  The end products Teacher 1 would get, would be lifeless replications of the teacher’s thinking!  While this might build some competence, it would not be supporting young creative writers.

Teacher 2 (giving different things to different groups) on the other hand would split the class into 3 or 4 groups and give everyone a different prompt.  “Some of you aren’t ready for this journal writing topic!!!”  Students in the high group would be allowed to be creative… students in the middle group wouldn’t be expected to be creative, but would have to do most of what is expected… and those in the “fix-up” group would be told exactly what to do and how to do it.  While this strategy might seem like targeted instruction, sadly those who might need the most help would be missing out on many of the important pieces of developing writers – including allowing them to be engaged and interested in the creative processes.

---

Teacher 1 might be helpful for some in the class because they are telling specific things that might be helpful for some.

Teacher 2 might be helpful for some of the students in the class too… especially those that might feel like they are the top group.

But something tells me, that neither are allowing their students to reach their potential!!!

---

Think again to the writing teacher I described at the beginning.  They weren’t overly prescriptive at first, but became more focused after they knew more about their students.  They provided EVERYONE opportunity to be creative and do the SAME task!

In math, the most effective strategy for differentiating instruction, in my opinion, is using open problems.  When a task is open, it allows all students to access the material, and allows all students to share what they currently understand.  However, this isn’t enough.  We then need to have some students share their thinking in a lesson close (this can include the timely and descriptive feedback everyone in the group needs).  Building the knowledge together is how we learn.  This also means that future problems / tasks should be built on what was just learned.

---

We know that to differentiate instruction is to allow for differences in the products, content and/or processes of learning… However, I think what might differ between teacher’s ability to use differentiated instruction strategies is if they are Teacher-Centered… or Student-Centered!

When we are teacher-centered we believe that it is our job to tell which students should be working on which things or aim to control which strategies each student will be learning.  However, I’m not convinced that we would ever be able to accurately know which strategies students are ready for (and therefore which ones we wouldn’t want them to hear), nor am I convinced that giving students different things regularly is healthy for our students.

Determining how to place students in groups is an important decision.  Avoid continually grouping by ability.  This kind of grouping, although well-intentioned, perpetuates low levels of learning and actually increases the gap between more and less dependent students.  Instead, consider using flexible grouping in which the size and makeup of small groups vary in a purposeful and strategic manner.  When coupled with the use of differentiation strategies, flexible grouping gives all students the chance to work successfully in groups. Van de Walle – Teaching Student Centered Mathematics

If we were to have students work on a problem in pairs, we need to be aware that grouping by ability as a regular practice can actually lead students to develop fixed mindsets – that is they start to recognize who is and who isn’t a math student.

---

Obviously there are times when some students need remediation, however, I think we are too quick to jump to remediation of skills instead of attempting to find ways to allow students to make sense of things in their own way followed by bringing the learning / thinking together to learn WITH and FROM each other.

---

To make these changes, however, I think we need to spend more time thinking about what a good problem or rich task should look like!  Maybe something for a future post?

---

As always, I want to leave you with a few reflective questions:

• I chose to compare what differentiated instruction looks like in mathematics to what it looks like in writing class.  However, I often hear more comparisons between reading and mathematics.  Do you see learning mathematics as an expressive subject like writing or a receptive subject like reading?
• Where do you find tasks / problems that offer all of your students both access and challenge (just like a good writing prompt)?  How do these offer opportunities for your students to vary their process, product and/or content?
• Once we provide open problems for our students, how do you leverage the reasoning and representations from some in the room to help others learn and grow?
• Math is very different than Literacy.  Reading and writing, for the most part, are skills, while mathematics is content heavy.  So how do you balance the need to continually learn new things with the need to continually make connections and build on previous understanding?
• What barriers are there to viewing differentiated instruction like this?  How can we help as an online community?

---

For more on this topic I encourage you to read How do we meet the needs of so many unique students in a mixed-ability classroom?  or take a look at our Ontario Ministry’s vision for Differentiated Instruction in math: Differentiating Mathematics Instruction

I’d love to continue the conversation.  Write a response, or send me a message on Twitter ( @markchubb3 ).

The Same… or Different?

For many math teachers, the single most difficult issue they face on a daily basis is how to meet the needs of so many students that vary greatly in terms of what they currently know, what they can do, their motivation, their personalities…  While there are many strategies to help here, most of the strategies used seem to lean in one of two directions:

1. Build knowledge together as a group; or
2. Provide individualized instruction based on where students currently are

---

Let’s take a closer look at each of these beliefs:

Those that believe the answer is providing all students with same tasks and experiences often do so because of their focus on their curriculum standards.  They believe the teacher’s role is to provide their students with tasks and experiences that will help all of their students learn the material.  There are a few potential issues with this approach though (i.e., what to do with students who are struggling, timing the lesson when some students might take much more time than others…).

On the other hand, others believe that the best answer is individualized instruction.  They believe that students are in different places in their understand and because of this, the teacher’s role is to continually evaluate students and provide them with opportunities to learn that are “just right” based on those evaluations.  It is quite possible that students in these classrooms are doing very different tasks or possibly the same piece of learning, but completely different versions depending on each student’s ability.  There are a few difficulties with this approach though (i.e., making sure all students are doing the right tasks, constantly figuring out various tasks each day, the teacher dividing their time between various different groups…).

 

---

There are two seemingly opposite educational ideals that some might see as competing when we consider the two approaches above:  Differentiated Instruction and Complexity Science.  However, I’m actually not sure they are that different at all!

 

For instance, the term “differentiated instruction” in relation to mathematics can look like different things in different rooms.  Rooms that are more traditional or “teacher centered” (let’s call it a “Skills Approach” to teaching) will likely sort students by ability and give different things to different students.

From Prime Leadership kit

If the focus is on mastery of basic skills, and memorization of facts/procedures… it only makes sense to do Differentiated Instruction this way.  DI becomes more like “modifications” in these classrooms (giving different students different work).  The problem is, that everyone in the class not on an IEP needs to be doing the current grade’s curriculum.  Really though, this isn’t differentiated instruction at all… it is “individualized instruction”.  Take a look again at the Monograph: Differentiating Mathematics Instruction.

Differentiated instruction is different than this.  Instead of US giving different things to different students, a student-centered way of making this make sense is to provide our students with tasks that will allow ALL of our students have success.  By understanding Trajectories/Continuum/Landscapes of learning (See Cathy Fosnot for a fractions Landscape), and by providing OPEN problems and Parallel Tasks, we can move to a more conceptual/Constructivist model of learning!

Think about Writing for a moment.  We are really good at providing Differentiated Instruction in Writing.  We start by giving a prompt that allows everyone to be interested in the topic, students then write, we then provide feedback, and students continue to improve!  This is how math class can be when we start with problems and investigations that allow students to construct their own understanding with others!

---

The other theory at play here is Complexity Science.  This theory suggest that the best way for us to manage the needs of individual students is to focus on the learning of the class.

What Complexity Science Tells us about Teaching and Learning

 

The whole article is linked here if you are interested.  But basically, it outlines a few principles to help us see how being less prescriptive in our teaching, and being more purposeful in our awareness of the learning that is actually happening in our classrooms  will help us improve the learning in our classrooms.  Complexity Science tells us to think about how to build SHARED UNDERSTANDING as a group through SHARED EXPERIENCES.  Ideally we should start any new concept with problem solving opportunities so we can have the entire group learn WITH and FROM each other.  Then we should continue to provide more experiences for the group that will build on these experiences.

---

Helping all of the students in a mixed ability classroom thrive isn’t about students having choice to do DIFFERENT THINGS all of the time, nor is it about US choosing the learning for them… it should often be about students all doing the SAME THING in DIFFERENT WAYS.  When we share our differences, we learn FROM and WITH each other.  Learning in the math classroom should be about providing rich learning experiences, where the students are doing the thinking/problem solving.  Of course there are opportunities for students to consolidate and practice their learning independently, but that isn’t where we start.  We need to start with the ideas from our students.  We need to have SHARED EXPERIENCES (rich problems) for us to all learn from.

---

 

As always, I leave you with a few questions for you to consider:

• How do you make sure all of your students are learning?
• Who makes the decisions about the difficulty or complexity of the work students are doing?
• Are your students learning from each other?  How can you capitalize on various students’ strengths and ideas so your students can learn WITH and FROM each other?
• How can we continue to help our students make choices about what they learn and how they demonstrate their understanding?
• Do you see the relationship between Differentiated Instruction and the development of mathematical reasoning / creative thinking?  How can we help our students see mathematics as a subject where reasoning is the primary goal?
• How can we foster playful experience for our students to learn important mathematics and effectively help all of our students develop at the same time?
• What is the same for your students?  What’s different?

I’d love to continue the conversation.  Write a response, or send me a message on Twitter (@markchubb3).

How do we meet the needs of so many unique students in a mixed-ability classroom?

Explaining what something is can be really hard to do without that person actually experiencing the same thing as you.  One strategy that we often use to explain difficult concepts in math is to discuss non-examples.  Consider how the frayer model below could be used with any difficult concept you are discussing in class.

If we discussed fractions in class, many students might believe that they understand the concept, however, they might be over-generalizing.  Seeing non-examples would help all gain a much clearer idea of what fractions are.  Of the shapes below, which ones have 1/2 or 1/4 of the area shaded blue?  Which ones do not represent 1/2 or 1/4 of the shapes’ area?

Having students complete activities like this would be an excellent way for you to originally see students’ understanding, and then see students refine and develop ideas throughout the unit (they can continually add different models and correct misconceptions)

---

The purpose of this post, however, isn’t about fractions or even a Frayer Model.  I am actually writing about the often used phrase “Differentiated Instruction” (DI).  Hopefully we can think more about what DI looks like in our math classes by thinking about what DI is and isn’t.

---

How would you define Differentiated Instruction?

Take a look at the following graphic created by ASCD helping us think about what DI is and isn’t.

In many places, DI is looked at as grouping students by ability, or providing individualized instruction.  However, if you look at the graphic above, these are in the non-example section.  These views are probably more common in highly teacher-centered classrooms, where the teacher feels like they need to be in control of every student’s process, products and content.  For me, I don’t see how it is possible to have every student doing the same thing at the same time, or how productive it would be if we assigned different students to do different work (sounds like an access and equity issue here).

---

So how do we help all of our students in a mixed ability classroom???

First of all, a few words from Van de Walle’s Teaching Student Centered Mathematics p.43:

“All [students} do not learn the same thing in the same way at the same rate.  In fact, every classroom at every grade level contains a range of students with varying abilities and backgrounds.  Perhaps the most important work of teachers today is to be able to plan (and teach) lessons that support and challenge ALL students to learn important mathematics.

Teachers have for some time embraced the notion that students vary in reading ability, but the idea that students can and do vary in mathematical development may be new.  Mathematics education research reveals a great deal of evidence demonstrating that students vary in their understanding of specific mathematical ideas.  Attending to these differences in students’ mathematical development is key to differentiating mathematics instruction for your students.

Interestingly, the problem-based approach to teaching is the best way to teach mathematics while attending to the range of students in your classroom.  In a traditional, highly directed lesson, it is often assumed that all students will understand and use the same approach and the same ideas as determined by the teacher.  Students not ready to understand the ideas presented by the teacher must focus their attention on following rules or directions without developing a conceptual or relational understanding (Skemp, 1978).  This, of course, leads to endless difficulties and can leave students with misunderstandings or in need of significant remediation.  In contrast, in a problem-based classroom, students are expected to approach problems in a variety of ways that make sense to them, bringing to each problem the skills and ideas that they own.  So, with a problem-based approach to teaching mathematics, differentiation is already built in to some degree.“

---

When we take a student centered view of Differentiated Instruction, we start to see that all students can be given the SAME work, yet each individual student will be able to adjust the process, product and/or content naturally.  However, this requires us to start with things where students are going to make sense of them.  It requires us to move our instruction from a teaching FOR problem solving approach to a teaching THROUGH problem solving approach.  It requires us to offer things that are actually problems, not just practicing skills in contexts.

---

3 Strategies for Differentiating Instruction:

There seem to be 3 different ways we can help all of our students access to the same curriculum expectations, while attending to the various differences in our students:

1. Open-Middle Problems
2. Open-Ended Problems
3. Parallel Problems

Open-middle problems, or open routed problems as they are sometimes called, typically have 1 possible solution, however, there are several different strategies or pathways to reach the solution.  These are a great way for us to offer something that everyone will have access to.  Ideally, these problems need to have an entry point that all students enter into the problem with, yet offer extensions for all.  The benefit of this type of problem is that we can listen to and learn from our students about the strategies they use.  We can then use the 5 Practices as a way to move instruction forward based on our assessments.

Open-ended problems, on the other hand, typically have multiple plausible answers.   These problems, in contrast, offer a much wider range of content.  Again, the benefit of this type of problem is that we can listen to and learn from our students about the types of thinking they are currently using, and from there, consider what they are ready for next.  Again, we can then use the 5 Practices as a way to move instruction forward based on our assessments.

Parallel Problems differ from the other two types in that we are actually offering different things for our students to work on.  Hopefully, our students are given choice here as to which path they are taking, so we don’t run into the issue earlier posted about DI not being about ability grouping.  Parallel problems are aptly named because while some of the pathways are easier than others, all pathways are designed to meet the same curricular expectations (content standards).  Again though, we should be using the 5 Practices as a way to share student thinking with each other so our students can learn WITH and FROM each other and so we can move instruction forward based on our assessments.

---

For an in depth understanding of how these help us, please read the article entitled Differentiating Mathematics Instruction.

---

As always, I want to leave you with a few reflective questions:

• How do you balance the need to teach 1 set of standards with the responsibility of meeting your students where they are?
• Do you hear student centered messages like the ones I’ve posted here about DI, or more teacher centered messages?  Which set of messages do you believe is easier for you to attempt as a teacher?  Which set of messages would you believe would make the learning in your classroom richer?
• Who tends to participate in your classrooms?  Who tends to not participate?  How can the DI strategies above help change this dynamic so that the voices being heard in your classroom are more distributed?
• What issues do you see being a barrier to DI looking like this?  How can the online community help?

I’d love to continue the conversation.  Write a response, or send me a message on Twitter (@markchubb3).