Whose problems? Whose game? Whose puzzle?

TRU Math (Teaching for Robust Understanding) a few years ago shared their thoughts about what makes for a “Powerful Classroom”. Here are their 5 dimensions:

Looking through the dimensions here, it is obvious that some of these dimensions are discussed in detail in professional development sessions and in teacher resources. However, the dimension of Agency, Authority and Identity is often overlooked – maybe because it is much more complicated to discuss. Take a look at what this includes:

This dimension helps us as teachers consider our students’ perspectives. How are they experiencing each day? We should be reflecting on:

• Who has a voice? Who doesn’t?
• How are ideas shared between and among students?
• Who feels like they have contributed? Who doesn’t?
• Who is actively contributing? Who isn’t?

Reflecting on our students’ experiences makes us better teachers! So, I’ve been wondering:

Who created today’s problem / game / puzzle?

For most students, math class follows the same pattern:

This pattern of a lesson leaves many students disinterested, because they are not actively involved in the learning – which might lead to typical comments like, “When will we ever need this?”. This lesson format is TEACHER centered because it centers the teachers’ ideas (the teacher provides the problem, the teacher helps students, the teacher tells you if you are correct). In this example, students’ mathematical identities are not fostered. There is NO agency afforded to students. Authority solely belongs to the teachers. But there are ways to make identity / agency / authority a focus!

STUDENT driven ideas

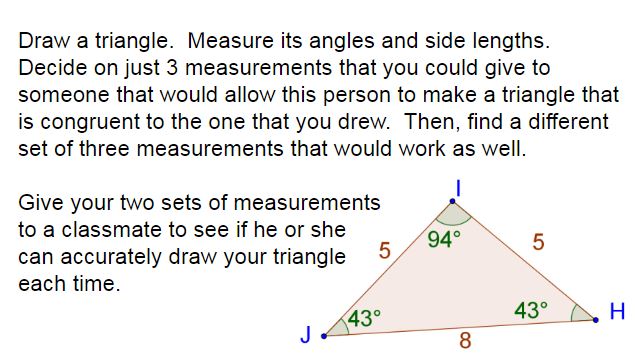
Today as a quick warm-up, I had students solve a little pentomino puzzle.  After they finished, I asked students to create their own puzzles that others will solve.  Here is one of the student created puzzles:

Here you can see a simple puzzle. The pieces are shown that you must use, and the board is included (with a hole in the middle). Now, as a class, we have a bank of puzzles we can attempt any day (as a warm-up or if work is finished).

You can read about WHY we would do puzzles like this in math class along with some examples (Spatial Reasoning).  

What’s more important here is for us to reflect on how we are involving our own students in the creation of problems, games and puzzles in our class.  This is a low-risk way to allow everyone in class do more than just participate, they are taking ownership in their learning, and building a community of learners that value learning WITH and FROM each other!

How to involve our students?

The example above shows us a simple way to engage our students, to expand what we consider mathematics and help our students form positive mathematical identities. However, there are lots of ways to do this:

• Play a math game for a day or 2, then ask students to alter one or a few of the rules.
• Have students submit questions you might want to consider for an assessment opportunity.
• Have students look through a bank or questions / problems and ask which one(s) would be the most important ones to do.
• Give students a sheet of many questions. Ask them to only do the 3 easiest, and the 3 hardest (then lead a discussion about what makes those ones the hardest).
• Lead 3-part math lessons where students start by noticing / wondering.
• Have students design their own SolveMe mobile puzzles, visual patterns, Which One Doesn’t Belong…

Questions to Reflect on:

• Who is not contributing in your class, or doesn’t feel like they are a “math student”? Whose mathematical identities would you like to foster? How might something simple like this make a world of difference for those children?
• Does it make a difference WHO develops the thinking?
• Fostering student identities, paying attention to who has authority in your class and allowing students to take ownership is essential to build mathematicians. The feeling of belonging in this space is crucial. How are you paying attention to this? (See Matthew Effect)
• How might these ideas help you meet the varied needs within a mixed ability classroom?
• If you do have your students create their own puzzles, will you first offer a simplified version so your students get familiar with the pieces, or will you dive into having them make their own first?
• Would you prefer all of your students doing the same puzzle / game / problem, or have many puzzles / games / problems to choose from? How might this change class conversations afterward?
• As the teacher, what will you be doing when students are playing? How might listening to student thinking help you learn more about your students? (See: Noticing and Wondering: A powerful tool for assessment)

I’d love to continue the conversation about students’ identities in mathematics.  Leave a comment here or on Twitter @MarkChubb3

Reasoning & Proving

This week I had the pleasure to see Dan Meyer, Cathy Fosnot and Graham Fletcher at OAME’s Leadership conference.

Each of the sessions were inspiring and informative… but halfway through the conference I noticed a common message that the first 2 keynote speakers were suggesting:

Dan Meyer showed us several examples of what mathematical surprise looks like in mathematics class (so students will be interested in making sense of what they are learning, and to get our students really thinking), while Cathy Fosnot shared with us how important it is for students to be puzzled in the process of developing as young mathematicians.  Both messages revolved around what I would consider the most important Process Expectation in the Ontario curriculum – Reasoning and Proving.

---

Reasoning and Proving

While some see Reasoning and Proving as being about how well an answer is constructed for a given problem – how well communicated/justified a solution is – this is not at all how I see it.  Reasoning is about sense-making… it’s about generalizing why things work… it’s about knowing if something will always, sometimes or never be true…it is about the “that’s why it works” kinds of experiences we want our students engaged in.  Reasoning is really what mathematics is all about.  It’s the pursuit of trying to help our students think mathematically (hence the name of my blog site).

---

A Non-Example of Reasoning and Proving

In the Ontario curriculum, students in grade 7 are expected to be able to:

• identify, through investigation, the minimum side and angle information (i.e.,side-side-side; side-angle-side; angle-side-angle) needed to describe a unique triangle

Many textbooks take an expectation like this and remove the need for reasoning.  Take a look:

As you can see, the textbook here shares that there are 3 “conditions for congruence”.  It shares the objective at the top of the page.  Really there is nothing left to figure out, just a few questions to complete.  You might also notice, that the phrase “explain your reasoning” is used here… but isn’t used in the sense-making way suggested earlier… it is used as a synonym for “show your work”.  This isn’t reasoning!  And there is no “identifying through investigation” here at all – as the verbs in our expectation indicate!

---

A Example of Reasoning and Proving

Instead of starting with a description of which sets of information are possible minimal information for triangle congruence, we started with this prompt:

Given a few minutes, each student created their own triangles, measured the side lengths and angles, then thought of which 3 pieces of information (out of the 6 measurements they measured) they would share.  We noticed that each successful student either shared 2 angles, with a side length in between the angles (ASA), or 2 side lengths with the angle in between the sides (SAS).  We could have let the lesson end there, but we decided to ask if any of the other possible sets of 3 pieces of information could work:

While most textbooks share that there are 3 possible sets of minimal information, 2 of which our students easily figured out, we wondered if any of the other sets listed above will be enough information to create a unique triangle.  Asking the original question didn’t offer puzzlement or surprise because everyone answered the problem without much struggle.  As math teachers we might be sure about ASA, SAS and SSS, but I want you to try the other possible pieces of information yourself:

Create triangle ABC where AB=8cm, BC=6cm, ∠BCA=60°

Create triangle FGH where ∠FGH=45°, ∠GHF=100°, HF=12cm

Create triangle JKL where ∠JKL=30°, ∠KLJ=70°, ∠LJK=80°

If you were given the information above, could you guarantee that everyone would create the exact same triangles?  What if I suggested that if you were to provide ANY 4 pieces of information, you would definitely be able to create a unique triangle… would that be true?  Is it possible to supply only 2 pieces of information and have someone create a unique triangle?  You might be surprised here… but that requires you to do the math yourself:)

---

Final Thoughts

Graham Fletcher in his closing remarks asked us a few important questions:

• Are you the kind or teacher who teaches the content, then offers problems (like the textbook page in the beginning)?  Or are you the kind of teacher who uses a problem to help your students learn?
• How are you using surprise or puzzlement in your classroom?  Where do you look for ideas?
• If you find yourself covering information, instead of helping your students learn to think mathematically, you might want to take a look at resources that aim to help you teach THROUGH problem solving (I got the problem used here in Marian Small’s new Open Questions resource).  Where else might you look?
• What does Day 1 look like when learning a new concept?
• Do you see Reasoning and Proving as a way to have students to show their work (like the textbook might suggest) or do you see Reasoning and Proving as a process of sense-making (as Marian Small shares)?
• Do your students experience moments of cognitive disequilibrium… followed by time for them to struggle independently or with a partner?  Are they regularly engaged in sense-making opportunities, sharing their thinking, debating…?
• The example I shared here isn’t the most flashy example of surprise, but I used it purposefully because I wanted to illustrate that any topic can be turned into an opportunity for students to do the thinking.  I would love to discuss a topic that you feel students can’t reason through… Let’s think together about if it’s possible to create an experience where students can experience mathematical surprise… or puzzlement… or be engaged in sense-making…  Let’s think together about how we can make Reasoning and Proving a focus for you and your students!

I’d love to continue the conversation.  Write a response, or send me a message on Twitter ( @markchubb3 ).

Reasoning and Proving

This week I had the pleasure to see Dan Meyer, Cathy Fosnot and Graham Fletcher at OAME’s Leadership conference.

Each of the sessions were inspiring and informative… but halfway through the conference I noticed a common message that the first 2 keynote speakers were suggesting:

Dan Meyer showed us several examples of what mathematical surprise looks like in mathematics class (so students will be interested in making sense of what they are learning), while Cathy Fosnot shared with us how important it is for students to be puzzled in the process of developing as young mathematicians.  Both messages revolved around what I would consider the most important Process Expectation in the Ontario curriculum – Reasoning and Proving.

---

Reasoning and Proving

While some see Reasoning and Proving as being about how well an answer is constructed for a given problem – how well communicated/justified a solution is – this is not at all how I see it.  Reasoning is about sense-making… it’s about generalizing why things work… it’s about knowing if something will always, sometimes or never be true…it is about the “that’s why it works” kinds of experiences we want our students engaged in.  Reasoning is really what mathematics is all about.  It’s the pursuit of trying to help our students think mathematically (hence the name of my blog site).

---

A Non-Example of Reasoning and Proving

In the Ontario curriculum, students in grade 7 are expected to be able to:

• identify, through investigation, the minimum side and angle information (i.e.,side-side-side; side-angle-side; angle-side-angle) needed to describe a unique triangle

Many textbooks take an expectation like this and remove the need for reasoning.  Take a look:

As you can see, the textbook here shares that there are 3 “conditions for congruence”.  It shares the objective at the top of the page.  Really there is nothing left to figure out, just a few questions to complete.  You might also notice, that the phrase “explain your reasoning” is used here… but isn’t used in the sense-making way suggested earlier… it is used as a synonym for “show your work”.  This isn’t reasoning!  And there is no “identifying through investigation” here at all – as the verbs in our expectation indicate!

---

A Example of Reasoning and Proving

Instead of starting with a description of which sets of information are possible minimal information for triangle congruence, we started with this prompt:

Given a few minutes, each student created their own triangles, measured the side lengths and angles, then thought of which 3 pieces of information (out of the 6 measurements they measured) they would share.  We noticed that each successful student either shared 2 angles, with a side length in between the angles (ASA), or 2 side lengths with the angle in between the sides (SAS).  We could have let the lesson end there, but we decided to ask if any of the other possible sets of 3 pieces of information could work:

While most textbooks share that there are 3 possible sets of minimal information, 2 of which our students easily figured out, we wondered if any of the other sets listed above will be enough information to create a unique triangle.  Asking the original question didn’t offer puzzlement or surprise because everyone answered the problem without much struggle.  As math teachers we might be sure about ASA, SAS and SSS, but I want you to try the other possible pieces of information yourself:

Create triangle ABC where AB=8cm, BC=6cm, ∠BCA=60°

Create triangle FGH where ∠FGH=45°, ∠GHF=100°, HF=12cm

Create triangle JKL where ∠JKL=30°, ∠KLJ=70°, ∠LJK=80°

If you were given the information above, could you guarantee that everyone would create the exact same triangles?  What if I suggested that if you were to provide ANY 4 pieces of information, you would definitely be able to create a unique triangle… would that be true?  Is it possible to supply only 2 pieces of information and have someone create a unique triangle?  You might be surprised here… but that requires you to do the math yourself:)

---

Final Thoughts

Graham Fletcher in his closing remarks asked us a few important questions:

• Are you the kind or teacher who teaches the content, then offers problems (like the textbook page in the beginning)?  Or are you the kind of teacher who uses a problem to help your students learn?
• How are you using surprise or puzzlement in your classroom?  Where do you look for ideas?
• If you find yourself covering information, instead of helping your students learn to think mathematically, you might want to take a look at resources that aim to help you teach THROUGH problem solving (I got the problem used here in Marian Small’s new Open Questions resource).  Where else might you look?
• What does Day 1 look like when learning a new concept?
• Do you see Reasoning and Proving as a way to have students to show their work (like the textbook might suggest) or do you see Reasoning and Proving as a process of sense-making (as Marian Small shares)?
• Do your students experience moments of cognitive disequilibrium… followed by time for them to struggle independently or with a partner?  Are they regularly engaged in sense-making opportunities, sharing their thinking, debating…?
• The example I shared here isn’t the most flashy example of surprise, but I used it purposefully because I wanted to illustrate that any topic can be turned into an opportunity for students to do the thinking.  I would love to discuss a topic that you feel students can’t reason through… Let’s think together about if it’s possible to create an experience where students can experience mathematical surprise… or puzzlement… or be engaged in sense-making…  Let’s think together about how we can make Reasoning and Proving a focus for you and your students!

I’d love to continue the conversation.  Write a response, or send me a message on Twitter ( @markchubb3 ).

Rushing for Interventions

I see students working in groups all the time…  Students working collaboratively in pairs or small groups having rich discussions as they sort shapes by specific properties, students identifying and extending their partner’s visual patterns, students playing games aimed at improving their procedural fluency, students cooperating to make sense of a low-floor/high-ceiling problem…..

When we see students actively engaged in rich mathematics activities, working collaboratively, it provides opportunities for teachers to effectively monitor student learning (notice students’ thinking, provide opportunities for rich questioning, and lead to important feedback and next steps…) and prepare the teacher for the lesson close.  Classrooms that engage in these types of cooperative learning opportunities see students actively engaged in their learning.  And more specifically, we see students who show Agency, Ownership and Identity in their mathematics learning (See TruMath‘s description on page 10).

---

On the other hand, some classrooms might be pushing for a different vision of what groups can look like in a mathematics classroom.  One where a teachers’ role is to continually diagnose students’ weaknesses, then place students into ability groups based on their deficits, then provide specific learning for each of these groups.  To be honest, I understand the concept of small groups that are formed for this purpose, but I think that many teachers might be rushing for these interventions too quickly.

First, let’s understand that small group interventions have come from the RTI (Response to Intervention) model.  Below is a graphic created by Karen Karp shared in Van de Walle’s Teaching Student Centered Mathematics to help explain RTI:

Response to Intervention – Teaching Student Centered Mathematics

As you can see, given a high quality mathematics program, 80-90% of students can learn successfully given the same learning experiences as everyone.  However, 5-10% of students (which likely are not always the same students) might struggle with a given topic and might need additional small-group interventions.  And an additional 1-5% might need might need even more specialized interventions at the individual level.

The RTI model assumes that we, as a group, have had several different learning experiences over several days before Tier 2 (or Tier 3) approaches are used.  This sounds much healthier than a model of instruction where students are tested on day one, and placed into fix-up groups based on their deficits, or a classroom where students are placed into homogeneous groupings that persist for extended periods of time.

---

Principles to Action (NCTM) suggests that what I’m talking about here is actually an equity issue!

Principles to Action

We know that students who are placed into ability groups for extended periods of time come to have their mathematical identity fixed because of how they were placed.  That is, in an attempt to help our students learn, we might be damaging their self perceptions, and therefore, their long-term educational outcomes.

---

Tier 1 Instruction

While I completely agree that we need to be giving attention to students who might be struggling with mathematics, I believe the first thing we need to consider is what Tier 1 instruction looks like that is aimed at making learning accessible to everyone.  Tier 1 instruction can’t simply be direct instruction lessons and whole group learning.  To make learning mathematics more accessible to a wider range of students, we need to include more low-floor/high-ceiling tasks, continue to help our students spatalize the concepts they are learning, as well as have a better understanding of developmental progressions so we are able to effectively monitor student learning so we can both know the experiences our students will need to be successful and how we should be responding to their thinking.  Let’s not underestimate how many of our students suffer from an “experience gap”, not an “achievement gap”!

If you are interested in learning more about what Tier 1 instruction can look like as a way to support a wider range of students, please take a look at one of the following:

•  How do we meet the needs of so many unique students in a mixed-ability classroom?
• Differentiated Instruction: comparing 2 subjects
• Differentiating Mathematics Instruction

---

Tier 2 Instruction

Tier 2 instruction is important.  It allows us to give additional opportunities for students to learn the things they have been learning over the past few days/weeks in a small group.  Learning in a small group with students who are currently struggling with the content they are learning can give us opportunities to better know our students’ thinking.  However, I believe some might be jumping past Tier 1 instruction (in part or completely) in an attempt to make sure that we are intervening. To be honest, this doesn’t make instructional sense to me! If we care about our content, and care about our students’ relationship with mathematics, this might be the wrong first move.

So, let’s make sure that Tier 2 instruction is:

• Provided after several learning experiences for our students
• Flexibly created, and easily changed based on the content being learned at the time
• Focused on student strengths and areas of need, not just weaknesses
• Aimed at honoring students’ agency, ownership and identity as mathematicians
• Temporary!

If you are interested in learning more about what Tier 2 interventions can look like take a look at one of the following:

• RTI for Adults
• Targeted Instruction
• Continuing to get better together

---

Instead of seeing mathematics as being learned every day as an approach to intervene, let’s continue to learn more about what Tier 1 instruction can look like!  Or maybe you need to hear it from John Hattie:

Or from Jo Boaler:

---

Final Thoughts

If you are currently in a school that uses small group instruction in mathematics, I would suggest that you reflect on a few things:

• How do your students see themselves as mathematicians?  How might the topics of Agency, Authority and Identity relate to small group instruction?
• What fixed mindset messaging do teachers in your building share “high kids”, “level 2 students”, “she’s one of my low students”….?  What fixed mindset messages might your students be hearing?
• When in a learning cycle do you employ small groups?  Every day?  After several days of learning a concept?
• How flexible are your groups?  Are they based on a wholistic leveling of your students, or based specifically on the concept they are learning this week?
• How much time do these small groups receive?  Is it beyond regular instructional timelines, or do these groups form your Tier 1 instructional time?
• If Karp/Van de Walle suggests that 80-90% of students can be successful in Tier 1, how does this match what you are seeing?  Is there a need to learn more about how Tier 1 approaches can meet the needs of this many students?
• What are the rest of your students doing when you are working with a small group?  Is it as mathematically rich as the few you’re working with in front of you?
• Do you believe that all of your students are capable to learn mathematics and to think mathematically?

I’d love to continue the conversation.  Write a response, or send me a message on Twitter ( @markchubb3 ).

Professional Development: What should it look like?

A few weeks ago Michael Fenton asked on his blog this question:

Suppose a teacher gets to divide 100% between two categories: teaching ability and content knowledge. What’s the ideal breakdown?

The question sparked many different answers that showed a very wide range of thinking, from 85%/15% favouring content, to 100% favouring pedagogy.  In general though, it seems that more leaned toward the pedagogy side than the content side.  While each response articulated some of their own experiences or beliefs, I wonder if we are aware of just how much content and pedagogical knowledge we come into this conversation with, and whether or not we have really thought about what each entails?  Let’s consider for a moment what these two things are:

---

What is Content Knowledge?

To many, the idea of content knowledge is simple.  It involves understanding the concept or skill yourself.  However, I don’t believe it is that simple!  Liping Ma has attempted to define what content knowledge is in her book:  Knowing and Teaching Elementary Mathematics: Teachers’ Understanding of Fundamental Mathematics in China & the United States.  In her book she describes teachers that have a Profound Understanding of Fundamental Mathematics (or PUFM) and describes those teachers as having the following characteristics:

Connectedness – the teacher feels that it is necessary to emphasize and make explicit connections among concepts and procedures that students are learning. To prevent a fragmented experience of isolated topics in mathematics, these teachers seek to present a “unified body of knowledge” (Ma, 1999, p.122).

Multiple Perspectives – PUFM teachers will stress the idea that multiple solutions are possible, but also stress the advantages and disadvantages of using certain methods in certain situations. The aim is to give the students a flexible understanding of the content.

Basic Ideas – PUFM teachers stress basic ideas and attitudes in mathematics. For example, these include the idea of an equation, and the attitude that single examples cannot be used as proof.

Longitudinal Coherence – PUFM teachers are fundamentally aware of the entire elementary curriculum (and not just the grades that they are teaching or have taught). These teachers know where their students are coming from and where they are headed in the mathematics curriculum. Thus, they will take opportunities to review what they feel are “key pieces” in knowledge packages, or lay appropriate foundation for something that will be learned in the future.

Taken from this Yorku wiki

As you can see, having content knowledge means far more than making sure that you understand the concept yourself.  To have rich content knowledge means that you have a deep understanding of the content.  It means that you understand which models and visuals might help our students bridge their understanding of concepts and procedures, and when we should use them.  Content knowledge involves a strong developmental and interconnected grasp of the content, and beliefs about what is important for students to understand.  Those that have strong content knowledge, have what is known as a “relational understanding” of the material and strong beliefs about making sure their students are developing a relational understanding as well!

---

What is Pedagogical Knowledge?

Pedagogical knowledge, on the other hand, involves the countless intentional decisions we make when we are in the act of teaching.  While many often point out essential components like classroom management, positive interactions with students… let’s consider for a moment the specific to mathematics pedagogical knowledge that is helpful.  Mathematical pedagogical knowledge includes:

• Understanding how to help students construct knowledge and a belief that constructivist principles are necessary to help all students be successful;
• Setting up a classroom atmosphere where clear and productive norms are present;
• Strategies to help promote thinking and discourse in all students (i.e., practices for orchestrating productive conversations, importance of wait time, cooperative learning opportunities…);
•  Strategies to help students when they are struggling (i.e., asking effective questions, knowing when to give new/different experiences…);
• Strategies to consolidate the learning during a lesson close;
• Strategies that promote productive struggle;
• Strategies to help students receive and act on feedback regularly.

---

Which is More Important:  Pedagogy or Content Knowledge?

Tracy Zager during last year’s Twitter Math Camp (Watch her TMC16 keynote address here) showed us Ben Orlin’s graphic explaining his interpretation of the importance of Pedagogy and Content Knowledge.  Take a look:

In Ben’s post, he explains that teachers who teach younger students need very little content knowledge, and a strong understanding of pedagogy.  However, in the video, Tracy explains quite articulately how this is not at all the case (if you didn’t watch her video linked above, stop reading and watch her speak – If pressed for time, make sure you watch minutes 9-14).

In the end, we need to recognize just how important both pedagogy and content are no matter what grade we teach.  Kindergarten – grade 2 teachers need to continually deepen their content knowledge too!  Concepts that are easy for us to do like counting, simple operations, composing/decomposing shapes, equality… are not necessarily easy for us to teach.  That is, just because we can do them, doesn’t mean that we have a Profound Understanding of Foundational Mathematics.  Developing our Content Knowledge requires us to understand the concepts in a variety of ways, to deepen our understanding of how those concepts develop over time so we don’t leave experiential gaps with our students!  

However, I’m not quite sure that the original question from Michael or that presented by Ben accurately explain just how complicated it is to explain what we need to know and be able to do as math teachers.  Debra Ball explains this better than anyone I can think of.  Take a look:

Research Gate: Figure 1.  Mathematical Knowledge for Teaching (Ball et., al, 2008)

Above is a visual that explains the various types of knowledge, according to Deb Ball, that teachers need in order to effectively teach mathematics.  Think about how your own knowledge fits in above for a minute.  Which sections would you say you are stronger in?  Which ones would you like to continue to develop?

Hopefully you are starting to see just how interrelated Content and Pedagogy are, and how ALL teachers need to be constantly improving in each of the areas above if we are to provide better learning opportunities for our students!

---

 What should Professional Development Look Like?

The purpose of this article is actually about professional development, but I felt it necessary to start by providing the necessary groundwork before tackling a difficult topic like professional development.

Considering just how important and interrelated Content Knowledge and Pedagogy are for teaching, I wonder what the balance is in the professional development currently in your area?  What would you like it to look like?  What would you like to learn?

While the theme here is about effective PD, I’m actually not sure I can answer my own question.  First of all, I don’t think PD should always look the same way for all teachers, in all districts, for all concepts.  And secondly, I’m not sure that even if we found the best form of PD it would be enough because we will constantly need new/different experiences to grow and learn.  I would like to offer, however, some of my current thoughts on PD and how we learn.

---

Some personal beliefs:

• We don’t know what we don’t know.  That is, given any simple concept or skill, there is likely an abundance of research, best practices, connections to other concepts/skills, visual approaches… that you are unaware of.  Professional development can help us learn about what we weren’t even aware we didn’t know about.
• Districts and schools tend to focus on pedagogy far more than content.  Topics like grading, how to assess, differentiated instruction… tend to be hot topics and are easier to monitor growth than the importance of helping our students develop a relational understanding.  However, each of those pedagogical decisions relies on our understanding of the content (i.e., if we are trying to get better at assessment, we need to have a better understanding of developmental trajectories/continuums so we know better what to look for).  The best way to understand any pedagogy is to learn about the content in new ways, then consider the pedagogy involved.
• Quality resources are essential, but handing out a resource is not the same as professional development.  Telling others to use a resource is not the same as professional development, no matter how rich the resource is!  Using a resource as a platform to learn things is better than explaining how to use a resource.  The goal needs to be our learning and hoping that we will act on our learning, not us doing things and hoping we will learn from it.
• The knowledge might not be in the room.  An old adage tells us that when we are confronted with a problem, that the knowledge is in the room.  However, I am not sure this is always the case.  If we are to continue to learn, we need experts helping us to learn!  Otherwise we will continually recycle old ideas and never learn anything new as a school/district.  If we want professional development, we need new ideas.  This can come in the form of an expert or more likely in the form of a resource that can help us consider content & pedagogy.
• Learning complicated things can’t be transmitted.  Having someone tell you about something is very different than experiencing it yourself.  Learning happens best when WE are challenged to think of things in ways we hadn’t before.  Professional development needs to be experiential for it to be effective!
• Experiencing learning in a new way is not enough.  Seeing a demonstration of a great teaching strategy, or being asked to do mental math and visually represent it, or experiencing manipulatives in ways you hadn’t previously experienced is a great start to learning, but it isn’t enough.  Once we have experienced something, we need to discuss it, think about the pedagogy and content involved, and come to a shared understanding of what was just learned.
• Professional learning can happen in a lot of different places and look like a lot of different things.  While many might assume that professional development is something that we sign up for in a building far from your own school, hopefully we can recognize that we can learn from others in a variety of contexts.  This happens when we show another teacher in our school what we are doing or what our students did on an assignment that we hadn’t expected.  It happens when we disagree on twitter or see something we would never have considered before.  We are engaging in professional development when we read a professional book or blog post that helps us to consider new things and especially when those things make us reconsider previous thoughts.  And professional learning especially happens when we get to watch others’ teach and then discuss what we noticed in both the teaching and learning of the material.
• Some of the best professional development happens when we are inquiring about teaching / learning together with others, and trying things out together!  When we learn WITH others, especially when one of the others is an expert, then take the time to debrief afterward, the learning can be transformational.
• Beliefs about how students learn mathematics best is true for adults too.  This includes beliefs about constructivist approaches, learning through problem solving, use of visual/spatial reasoning, importance of consolidating the learning, role of discourse…
• Not everyone gets the same things out of the same experiences.  Some people are reflecting much more than others during any professional learning experience.  Personally, I always try to make connections, think about the leaders’ motivations/beliefs, reflect on my own practices… even if the topic is something I feel like I already understand.  There is always room for learning when we make room for learning!

---

Some things to reflect on:

As always, I like to ask a few questions to help us reflect:

• Think of a time you came to make a change in your beliefs about what is important in teaching mathematics.  What led to that change?
• Think of a time you tried something new.  What helped you get started?
• Where do you get your professional learning?  Is your board / school providing the kind of learning you want/need?  If so, how do you take advantage of this more often?  If not, how could this become a reality?
• Think about your answers to any of the above questions.  Were you considering learning about pedagogy or content knowledge?  What does this say about your personal beliefs about professional development?
• Take a look again at any of the points I made under “Some Personal Beliefs”.  Is there one you have issue with?  I’d love some push-back or questions… that’s how we learn:)

As always, I encourage you to leave a message here or on Twitter (@markchubb3)!

The Same… or Different?

For many math teachers, the single most difficult issue they face on a daily basis is how to meet the needs of so many students that vary greatly in terms of what they currently know, what they can do, their motivation, their personalities…  While there are many strategies to help here, most of the strategies used seem to lean in one of two directions:

1. Build knowledge together as a group; or
2. Provide individualized instruction based on where students currently are

---

Let’s take a closer look at each of these beliefs:

Those that believe the answer is providing all students with same tasks and experiences often do so because of their focus on their curriculum standards.  They believe the teacher’s role is to provide their students with tasks and experiences that will help all of their students learn the material.  There are a few potential issues with this approach though (i.e., what to do with students who are struggling, timing the lesson when some students might take much more time than others…).

On the other hand, others believe that the best answer is individualized instruction.  They believe that students are in different places in their understand and because of this, the teacher’s role is to continually evaluate students and provide them with opportunities to learn that are “just right” based on those evaluations.  It is quite possible that students in these classrooms are doing very different tasks or possibly the same piece of learning, but completely different versions depending on each student’s ability.  There are a few difficulties with this approach though (i.e., making sure all students are doing the right tasks, constantly figuring out various tasks each day, the teacher dividing their time between various different groups…).

 

---

There are two seemingly opposite educational ideals that some might see as competing when we consider the two approaches above:  Differentiated Instruction and Complexity Science.  However, I’m actually not sure they are that different at all!

 

For instance, the term “differentiated instruction” in relation to mathematics can look like different things in different rooms.  Rooms that are more traditional or “teacher centered” (let’s call it a “Skills Approach” to teaching) will likely sort students by ability and give different things to different students.

From Prime Leadership kit

If the focus is on mastery of basic skills, and memorization of facts/procedures… it only makes sense to do Differentiated Instruction this way.  DI becomes more like “modifications” in these classrooms (giving different students different work).  The problem is, that everyone in the class not on an IEP needs to be doing the current grade’s curriculum.  Really though, this isn’t differentiated instruction at all… it is “individualized instruction”.  Take a look again at the Monograph: Differentiating Mathematics Instruction.

Differentiated instruction is different than this.  Instead of US giving different things to different students, a student-centered way of making this make sense is to provide our students with tasks that will allow ALL of our students have success.  By understanding Trajectories/Continuum/Landscapes of learning (See Cathy Fosnot for a fractions Landscape), and by providing OPEN problems and Parallel Tasks, we can move to a more conceptual/Constructivist model of learning!

Think about Writing for a moment.  We are really good at providing Differentiated Instruction in Writing.  We start by giving a prompt that allows everyone to be interested in the topic, students then write, we then provide feedback, and students continue to improve!  This is how math class can be when we start with problems and investigations that allow students to construct their own understanding with others!

---

The other theory at play here is Complexity Science.  This theory suggest that the best way for us to manage the needs of individual students is to focus on the learning of the class.

What Complexity Science Tells us about Teaching and Learning

 

The whole article is linked here if you are interested.  But basically, it outlines a few principles to help us see how being less prescriptive in our teaching, and being more purposeful in our awareness of the learning that is actually happening in our classrooms  will help us improve the learning in our classrooms.  Complexity Science tells us to think about how to build SHARED UNDERSTANDING as a group through SHARED EXPERIENCES.  Ideally we should start any new concept with problem solving opportunities so we can have the entire group learn WITH and FROM each other.  Then we should continue to provide more experiences for the group that will build on these experiences.

---

Helping all of the students in a mixed ability classroom thrive isn’t about students having choice to do DIFFERENT THINGS all of the time, nor is it about US choosing the learning for them… it should often be about students all doing the SAME THING in DIFFERENT WAYS.  When we share our differences, we learn FROM and WITH each other.  Learning in the math classroom should be about providing rich learning experiences, where the students are doing the thinking/problem solving.  Of course there are opportunities for students to consolidate and practice their learning independently, but that isn’t where we start.  We need to start with the ideas from our students.  We need to have SHARED EXPERIENCES (rich problems) for us to all learn from.

---

 

As always, I leave you with a few questions for you to consider:

• How do you make sure all of your students are learning?
• Who makes the decisions about the difficulty or complexity of the work students are doing?
• Are your students learning from each other?  How can you capitalize on various students’ strengths and ideas so your students can learn WITH and FROM each other?
• How can we continue to help our students make choices about what they learn and how they demonstrate their understanding?
• Do you see the relationship between Differentiated Instruction and the development of mathematical reasoning / creative thinking?  How can we help our students see mathematics as a subject where reasoning is the primary goal?
• How can we foster playful experience for our students to learn important mathematics and effectively help all of our students develop at the same time?
• What is the same for your students?  What’s different?

I’d love to continue the conversation.  Write a response, or send me a message on Twitter (@markchubb3).

Starting where our students are….. with THEIR thoughts

A common trend in education is to give students a diagnostic in order for us to know where to start. While I agree we should be starting where our students are, I think this can look very different in each classroom.  Does starting where our students are mean we give a test to determine ability levels, then program based on these differences?  Personally, I don’t think so.

Giving out a test or quiz at the beginning of instruction isn’t the ideal way of learning about our students.  Seeing the product of someone’s thinking often isn’t helpful in seeing HOW that child thinks (Read, What does “assessment drive instruction mean to you” for more on this). Instead, I offer an alternative- starting with a diagnostic task!  Here is an example of a diagnostic task given this week:

Taken from Van de Walle’s Teaching Student Centered Mathematics

This lesson is broken down into 4 parts.  Below are summaries of each:

---

Part 1 – Tell 1 or 2 interesting things about your shape

Start off in groups of 4.  One student picks up a shape and says something (or 2) interesting about that shape.

Here you will notice how students think about shapes. Will they describe the shape as “looking like a mountain” or “it’s an hourglass” (visualization is level 1 on Van Hiele’s levels of Geometric thought)… or will they describe attributes of that shape (this is level 2 according to Van Hiele)?

As the teacher, we listen to the things our students talk about so we will know how to organize the conversation later.

---

Part 2 – Pick 2 shapes.  Tell something similar or different about the 2 shapes.

Students randomly pick 2 shapes and either tell the group one thing similar or different about the two shapes. Each person offers their thoughts before 2 new shapes are picked.

Students who might have offered level 1 comments a minute ago will now need to consider thinking about attributes. Again, as the teacher, we listen for the attributes our students understand (i.e., number of sides, right angles, symmetry, number of vertices, number of pairs of parallel sides, angles….), and which attributes our students might be informally describing (i.e., using phrases like “corners”, or using gestures when attempting to describe something they haven’t learned yet).  See chart below for a better description of Van Hiele’s levels:

Van Hiele’s chart shared by NCTM

At this time, it is ideal to hold conversations with the whole group about any disagreements that might exist.  For example, the pairs of shapes above created disagreements about number of sides and number of vertices.  When we have disagreements, we need to bring these forward to the group so we can learn together.

---

Part 3 – Sorting using a “Target Shape”

Pick a “Target Shape”. Think about one of its attributes.  Sort the rest of the shapes based on the target shape.

The 2 groups above sorted their shapes based on different attributes. Can you figure out what their thinking is?  Were there any shapes that they might have disagreed upon?

---

Part 4 – Secret sort

Here, we want students to be able to think about shapes that share similar attributes (this can potentially lead our students into level 2 type thinking depending on our sort).  I suggest we provide shapes already sorted for our students, but sorted in a way that no group had just sorted the shapes. Ideally, this sort is something both in your standards and something you believe your students are ready to think about (based on the observations so far in this lesson).

---

In this lesson, we have noticed how our students think.  We could assess the level of Geometric thought they are currently using, or the attributes they are comfortable describing, or misconceptions that need to be addressed.  But, this lesson isn’t just about us gathering information, it is also about our students being actively engaged in the learning process!  We are intentionally helping our students make connections, reason and prove, learn/ revisit vocabulary, think deeper about specific attributes…

---

I’ve shared my thoughts about what I think day 1 should look like before for any given topic, and how we can use assessment to drive instruction, however, I wanted to write this blog about the specific topic of diagnostics.

In the above example, we listened to our students and used our understanding of our standards and developmental research to know where to start our conversations. As Van de Walle explains the purpose of formative assessment, we need to make our formative more like a streaming video, not just a test at the beginning!

If its formative, it needs to be ongoing… part of instruction… based on our observations, conversations, and the things students create…  This requires us to start with rich tasks that are open enough to allow everyone an entry point and for us to have a plan to move forward!

I’m reminded of Phil Daro’s quote:

For us to make these shifts, we need to consider our mindsets that also need to shift.  Statements like the following stand in the way of allowing our students to be actively engaged in the learning process starting with where they currently are:

• My students aren’t ready for…
• I need to start with the basics…
• My students have gaps in their…
• They don’t know the vocabulary yet…

These thoughts are counterproductive and lead to the Pygmalion effect (teacher beliefs about ability become students’ self-fulfilling prophecies).  When WE decide which students are ready for what tasks, I worry that we might be holding many of our students back!

If we want to know where to start our instruction, start where your students are in their understanding…with their own thoughts!!!!!  When we listen and observe our students first, we will know how to push their thinking!

An Unsolved Problem your Students Should Attempt

There are several great unsolved math problems that are perfect for elementary students to explore.  One of my favourites is the palindrome sums problem.
In case you aren’t familiar, a palindrome is a word, phrase, sentence or number that reads the same forward and backward.

The problem itself comes out of this conjecture:

If you take any number and add it to its inverse (numbers reversed), it will eventually become a palindrome.

Let’s take a look at the numbers 12, 46 and 95:

---

---

---

As you can see with the above examples, some numbers can become palindromes with 1 simple addition, like the number 12.  12 + 21 = 33.  Can you think of others that should take 1 step?  How did you know?

Other numbers when added to their inverse will not immediately become a palindrome, but by continuing the process, will eventually, like the numbers 46 and 95.  Which numbers do you think will take more than 1 step?

---

After going through a few examples with students about the process of creating palindromes, ask your students to attempt to see if the conjecture is true (If you take any number and add it to its inverse (numbers reversed), it will eventually become a palindrome).  Have them find out if each number from 0-99 will eventually become a palindrome. Ask students if they need to find the answer for each number?  Encourage them to make their own conjectures so they don’t need to do all of the calculations for each number.

---

Mathematically proficient students look closely to discern a pattern or structure. They notice if calculations are repeated, and look both for general methods and for shortcuts. (SMP 7)

Some students will notice:

• Some numbers will already be a palindrome
• If they have figured out 12 + 21… they will know 21 + 12.  So they don’t have to do all of the calculations.  Nearly half of the work will have already been completed.
• A pattern emerging in their answers … 44, 55, 66, 77, 88, 99, 121… and see this pattern regularly (well, almost)
• A pattern about when numbers will have 99 as a palindrome, or 121… 18+81 = 27+72 = 36+63…

---

Thinking about our decisions:

• What is the goal of this lesson?  (Practice with addition?  Looking for patterns?  Perseverance?  Making conjectures? …)
• Do we share some of the conjectures students are making during the time when students are working, or later in the closing of the lesson?  
• How will my students record their work?  Keep track of their answers?  Do I provide a 0-99 chart or ask them to keep track somehow?
• Will students work independently / in pairs / in small groups?  Why?
• Do I allow calculators?  Why or why not?  (think back to your goal)
• How will I share the conjectures or patterns noticed with the class?
• Are my students gaining practice DOING (calculations) or THINKING (noticing patterns and making conjectures)?  Which do you value?

The smallest of decisions can make the biggest of impacts for our students!  

---

So, at the beginning of this post I shared with you that this problem is currently unsolved.  While it is true that the vast majority of numbers have been proven to easily become palindromes, there are some numbers that require many steps (89 and 98 require 24 steps), and others that have never been proven to either work or not work (198 is the smallest number never proven either way).

---

Some final thoughts about this problem…

After using this problem with many different students I have noticed that many start to see that mathematics can be a much more intellectually interesting subject than they had previously experienced.  This problem asks students to notice things, make conjectures, try to prove their conjectures and be able to communicate their conjectures with others…  The problem provides students with the opportunity to both think and do.  It offers students from various ability levels access to the problem (low floor), and many different avenues to challenge those ready for it (high ceiling).  It tells students that math is still a living, growing subject… that all of the problems have not yet been figured out!  And probably the most important for me, it sends students messages about what it means to really do mathematics!

 

Taken from Marilyn Burns’ 50 Problem Solving Lessons resource

 

Focus on Relational Understanding

Forty years ago, Richard Skemp wrote one of the most important articles, in my opinion, about mathematics, and the teaching and learning of mathematics called Relational Understanding and Instrumental Understanding.  If you haven’t already read the article, I think you need to add this to your summer reading (It’s linked above).

Skemp quite nicely illustrates the fact that many of us have completely different, even contradictory definitions, of the term “understanding”.   Here are the 2 opposing definitions of the word “understanding”:

“Instrumental understanding” can be thought of as knowing the rules and procedures without understanding why those rules or procedures work. Students who have been taught instrumentally can perform calculations, apply procedures… but do not necessarily understand the mathematics behind the rules or procedures.

“Relational understanding”, on the other hand, can be thought of as understanding how and why the rules and procedures work.  Students who are taught relationally are more likely to remember the procedures because they have truly understood why they work, they are more likely to retain their understanding longer, more likely to connect new learning with previous learning, and they are less likely to make careless mistakes.

Think of the two types of understanding like this:

Shared by David Wees

Students who are taught instrumentally come to see mathematics as isolated pieces of knowledge. They are expected to remember procedures for each and every concept/skill.  Each new skill requires a new set of procedures.  However, those who are taught relationally make connections between and within concepts and skills.  Those with a relational understanding can learn new concepts easier, retain previous concepts, and are able to deviate from formulas/rules given different problems easier because of the connections they have made.

While it might seem obvious that relational understanding is best, it requires us to understand the mathematics in ways that we were never taught in order for us to provide the best experiences for our students. It also means that we need to start with our students’ current understandings instead of starting with the rules and procedures.

Skemp articulates how much of an issue this really is in our educational system when he explains the different types of mismatches that can occur between how students are taught, and how students learn.  Take a look:

Notice the top right quadrant for a second.  If a child wants to learn instrumentally (they only want to know the steps/rules to solve today’s problem) and the teacher instead offers tasks/problems that asks the child to think or reason mathematically, the student will likely be frustrated for the short term.  You might see students that lack perseverance, or are eager for assistance because they are not used to thinking for themselves.  However, as their learning progresses, they will come to make sense of their mathematics and their initial frustration will fade.

On the other hand, if a teacher teaches instrumentally but a child wants to learn relationally (they want/need to understand why procedures work) a more serious mismatch will exist.  Students who want to make sense of the concepts they are learning, but are not given the time and conditions to experience mathematics in this way will come to believe that they are not good at mathematics.  These students soon disassociate with mathematics and will stop taking math classes as soon as they can.  These students view themselves as “not a math person” because their experiences have not helped them make sense of the mathematics they were learning.

While the first mismatch might seem frustrating for us as teachers, the frustration is short lived. On the other hand, the second mismatch has life-long consequences!

---

I’ve been thinking about the various initiatives/ professional development opportunities… that I have been part of, or have been available online or through print that might help us think about how to move from an instrumental understanding to a relational understanding of mathematics.  Here are a few I want to share with you:

Phil Daro’s Against Answer Getting video highlights a few instrumental practices that might be common in some schools.  Below is the “Butterfly” method of adding fractions he shares as an “answer getting” strategy.  While following these simple steps might help our students get the answer to this question, Phil points out that these students will be unable to solve an addition problem with 3 fractions.  These students “understand” how to get the answer, but in no way understand how the answer relates to addends.

On the other hand, teachers who teach relationally provide their students with contexts, models (i.e, number lines, arrays…), manipulatives (i.e., cuisenaire rods, pattern blocks…) and visuals to help their students develop a relational understanding.  If you are interested in learning more about helping your students develop a relational understanding of fractions, take a look at a few resources that will help:

• Cathy Fosnot’s Minilessons
• Cathy Bruce’s Fraction Pathways
• Cathy Fosnot’s Best Buys, Ratios, and Rates – Addition and Subtraction of Fractions

---

Tina Cardone and a group of math teachers across Twitter (part of the #MTBoS) created a document called Nix The Tricks that points out several instrumental “tricks” that do not lead to relational understanding.  For example, “turtle multiplication” is an instrumental strategy that will not help our students understand the mathematics that is happening.  Students can draw a collar and place an egg below, but in no way will this help with future concepts!

Teachers focused on relational understanding again use representations that allow their students to visualize what is happening.  Connections between representations, strategies and the big ideas behind multiplication are developed over time.

Take a look at some wonderful resources that promote a relational understanding of multiplication:

• Cathy Fosnots Mini Lessons for Extending Multiplication and Division 
• Cathy Fosnot’s Muffle Truffles & Big Dinner units
• Sherry Parrish’s Number Talks
• Cathy Humphreys & Ruth Parker’s Making Number Talks Matter
• Alex Lawson’s What to Look For

Each of the above are developmental in nature, they focus on representations and connections.

---

So how do we make these shifts?  Here are a few of my thoughts:

1. Notice instrumental teaching practices.
2. Learn more about how to move from instrumental to relational teaching.
3. Align assessment practices to expect relational understanding.

---

Goal 1 – Notice instrumental teaching practices.

Many of these are easy to spot.  Here is a small sample from Pinterest:

The rules/procedures shared here ask students to DO without understanding.  The issue is that there are actually countless instrumental practices out there, so my goal is actually much harder than it seems.  Think about something you teach that involves rules or procedures.  How can you help your students develop a relational understanding of this concept?

---

Goal 2 – Learn more about how to move from instrumental to relational teaching.

I don’t think this is something we can do on our own.  We need the help of professional resources (Marian Small, Van de Walle, Fosnot, and countless others have helped produce resources that are classroom ready, yet help us to see mathematics in ways that we probably didn’t experience as students), mathematics coaches, and the insights of teachers across the world (there is a wonderful community on Twitter waiting to share and learn with you).

I strongly encourage you to look at chapter 1 of Van de Walle’s Teaching Student Centered Mathematics where it will give a clearer view of relational understanding and how to teach so our students can learn relationally.

However we are learning, we need to be able to make new connections, see the concepts in different ways in order for us to know how to provide relational teaching for our students.

---

Goal 3 – Align assessment practices to expect relational understanding.

This is something I hope to continue to blog about.  If we want our students to have a relational understanding, we need to be clear about what we expect our students to be able to do and understand.  Looking at developmental landscapes, continuums and trajectories will help here.  Below is Cathy Fosnot’s landscape of learning for multiplication and division.  While this might look complicated, there are many different representations, strategies and big ideas that our students need to experience to gain a relational understanding.

Investigating Multiplication and Division Grades 3-5

Asking questions or problems that expect relational understanding is key as well.  Take a look at one of Marian Small’s slideshows below.  Toward the end of each she shares the difference between questions that focus on knowledge and questions that focus on understanding.

• Marian Small’s 7&8 slideshow
• Marian Small’s 1,2&3 Slideshow
• Marian Small’s 4,5,6,7&8 Slideshow

---

I hope whatever your professional learning looks like this year (at school, on Twitter, professional reading…) there is a focus on helping build your relational understanding of the concepts you teach, and a better understanding of how to build a relational understanding for your students.  This will continue to be my priority this year!