Data management is becoming an increasingly important topic as our students try to make sense of news, social media posts, advertisements… Especially as more and more of these sources aim to try to convince you to believe something (intentionally or not).
Part of our job as math teachers needs to include helping our students THINK as they are collecting / organizing / analyzing data. For example, when looking at data we want our students to:
- Notice the writer’s choice of scale(s)
- Notice the decisions made for categories
- Notice which data is NOT included
- Notice the shape of the data and spatial / proportional connections (twice as much/many)
- Notice the choice of type of graph chosen
- Notice irregularities in the data
- Notice similarities among or between data
- Consider ways to describe the data as a whole (i.e., central tendency) or the story it is telling over time (i.e., trends)
While each of these points are important, I’d like to offer a way we can help our students explore the last piece from above – central tendencies.
Central Tendency Puzzle Templates
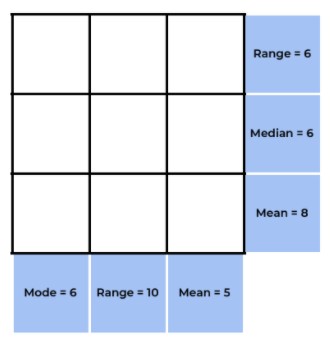
To complete each puzzle, you will need to make decisions about where to start, which numbers are most likely and then adjust based on what makes sense or not. I’d love to have some feedback on the puzzles.
Linked here are the Central Tendencies Puzzles.
Questions to Reflect on:
- How will your students be learning about central tendencies before doing these puzzles? What kinds of experience might lead up to these puzzles? (See A Few Simple Beliefs)
- How might puzzles like these offer your students practice for the skills they have been learning? (See purposeful practice)
- How might puzzles like this relate to playing Skyscraper puzzles?
- What is the current balance of questions / problems in your class? Are your students spending more time calculating, or deciding on which calculations are important? What balance would you like?
- How might these puzzles help you meet the varied needs within a mixed ability classroom?
- If students start to understand how to solve one of these, would you consider asking your students to make up their own puzzles? (Ideas for making your own problems here).
- How do these puzzles help your students build their mathematical intuitions? (See ideas here)
- Would you want students to work alone, in pairs, in groups? Why?
- Would you prefer all of your students doing the same puzzle / game / problem, or have many puzzles / games / problems to choose from? How might this change class conversations afterward?
- How will you consolidate the learning afterward? (See Never Skip the Closing of the Lesson)
- As the teacher, what will you be doing when students are playing? How might listening to student thinking help you learn more about your students? (See: Noticing and Wondering: A powerful tool for assessment)
I’d love to continue the conversation about these puzzles. Leave a comment here or on Twitter @MarkChubb3