What Makes Math Interesting Anyway?

Many teachers are comfortable allowing their students to read for pleasure at school and encourage reading at home for pleasure too. Writing is often seen as a creative activity. Our society appreciates Literacy as having both creative and purposeful aspects. Yet mathematics as a source of enjoyment or creativity is often not considered by many. 

I want you to reflect on your own thinking here. How important do you see creativity in mathematics? What does creativity in mathematics even mean to you?

Marian Small might explain the notion of creativity in mathematics best. Take a look:

Marian Small – Creativity and Mathematically Interesting Problems from Professional Learning Supports on Vimeo.

Type 1 and Type 2 Questions

Several years ago, Marian Small tried to help us as math teachers see what it means to think and be creative in mathematics by sharing 2 different ways for our students to experience the same content. She called them “type 1” and “type 2” questions.

Type 1 problems typically ask students to give us the answer.  There might be several different strategies used… There might be many steps or parts to the problem.  Pretty much every Textbook problem would fit under Type 1.  Every standardized test question would fit here.  Many “problem solving” type questions might fit here too.

Type 2 problems are a little tricky to define here. They aren’t necessarily more difficult, they don’t need a context, nor do they need to have more steps.  A Type 2 problem asks students to get to relationships about the concepts involved.  Essentially, Type 2 problems are about asking something where students could have plenty of possible answers (open ended). Again, here is Marian Small describing some examples:

Examples of Type 1 & 2 Questions

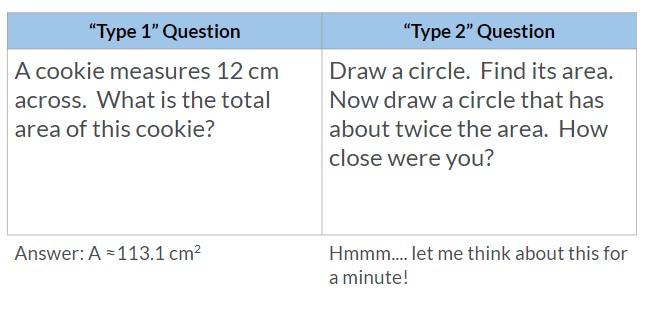
Notice that a type 2 problem is more than just open, it encourages you to keep thinking and try other possibilities!  The constraints are part of what makes this a “type 2” problem! The creativity and interest comes from trying to reach your goal!

Where do you look for “Type 2” Problems?

If you haven’t seen it before, the website called OpenMiddle.com is a great source of Type 2 problems.  Each involve students being creative to solve a potential problem AND start to notice mathematical relationships. 

Home

Remember, mathematically interesting problems (Type 2 problems) are interesting because of the mathematical connections, the relationships involved, the deepening of learning that occurs, not just a fancy context.

Questions to Reflect on:

• When do you include creativity in your math class? All the time? Daily? Toward the beginning of a unit? The end? What does this say about your program? (See A Few Simple Beliefs)
• If you find it difficult to create these types of questions, where do you look? Marian Small is a great start, but there are many places!
• How might “Type 2” problems like these offer your students practice for the skills they have been learning? (See purposeful practice)
• What is the current balance of q]Type 1 and Type 2 problems in your class? Are your students spending more time calculating, or deciding on which calculations are important? What balance would you like?
• How might problems like these help you meet the varied needs within a mixed ability classroom?
• If students start to understand how to solve type 2 problems, would you consider asking your students to make up their own problems? (Ideas for making your own problems here).
• How do these problems help your students build their mathematical intuitions? (See ideas here)
• Would you want students to work alone, in pairs, in groups? Why?
• If you have struggled with developing rich discussions in your class, how might these types of problems help you bring a need for discussions? How might this change class conversations afterward?
• How will you consolidate the learning afterward? (See Never Skip the Closing of the Lesson)
• As the teacher, what will you be doing when students are being creative? How might listening to student thinking help you learn more about your students? (See: Noticing and Wondering: A powerful tool for assessment)

I’d love to continue the conversation about creativity in mathematics.  Leave a comment here or on Twitter @MarkChubb3

The Types of Questions we Ask: which categories of questions should we focus on?

I think we can all agree that there are many different ways for our students to show what they know or understand, and that some problems ask for deeper understanding than others. In fact, many standardized math assessments, like PISA, aim to ask students questions at varying difficult levels (PISA uses 6 difficulty levels) to assess the same concept/skill. If we can learn one thing from assessments like these hopefully it is how to expect more of our students by going deeper… and in math class, this means asking better questions.

Robert Kaplinsky is a great example of an educator who has helped us better understand how to ask better questions. His work on Depth of Knowledge (DOK) has helped many teachers reflect on the questions they ask and has offered teachers examples of what higher DOK questions/problems look like.

In Ontario though we actually have an achievement chart that is aimed to help us think more about the types of questions/problems we expect our students be able to do. Basically, it is a rubric showing 4 levels of achievement across 4 categories. In Ontario it is expected that every teacher evaluate their students based on each the these categories. Many teachers, however, struggle to see the differences between these categories. Marian Small recently was the keynote speaker at OAME where she helped us think more about the categories by showing us how to delineate between the different categories of questions/problems:

• Knowledge
• Understanding
• Application
• Thinking

Knowledge vs. Understanding

Below are a few of Marian Small’s examples of questions that are designed to help us see the difference between questions aimed at knowledge and questions aimed at understanding:

As you can see from the above examples, each of the knowledge questions ask students to provide a correct answer. However, each of the understanding questions require students to both get a correct answer AND be able to show that they understand some of the key relationships involved. Marian’s point in showing us these comparisons was to tell us that we need to spend much more time and attention making sure our students understand the math they are learning.

Each of the questions that asks students to show their understanding also help us see what knowledge our students have, but the other way around is not true!

Hopefully you can see the potential benefits of striving for understanding, but I do believe these shifts need to be deliberate. My recommendation to help us aim for understanding is to ask more questions that ask students to:

• Draw a visual representation to show why something works
• Provide an example that fits given criteria
• Explain when examples will or won’t work
• Make choices (i.e., which numbers, visual representations… will be best to show proof)
• show their understanding of key “Big Ideas” and relationships

Application vs. Thinking

Below are a few examples that can help us delineate the differences between application and thinking:

These examples might be particularly important for us to think about. To begin with, application questions often use some or all of the following:

• use a context
• require students to use things they already should know
• provide a picture(s) or example(s) for students to see
• provide almost all of the information and ask the student to find what is missing

Thinking questions, on the other hand, are the basis for what Stein et. al called “Doing Mathematics“. In Marian’s presentation, she discussed with us that these types of questions are why those who enjoy mathematics like doing mathematics. Thinking and reasoning are at the heart of what mathematics is all about! Thinking questions typically require the student to:

• use non-algorithmic thinking
• make sense of the problem
• use relevant knowledge
• notice important features of the problem
• choose a possible solution path and possibly adjust if needed
• persevere to monitor their own progress

Let’s take a minute to compare questions aimed at application and questions aimed at thinking. Application questions, while quite helpful in learning mathematics concepts (contexts should be used AS students learn), they typically offer less depth than thinking questions. In each of the above application questions, a student could easily ignore the context and fall back on learned procedures. On the other hand, each of the thinking questions might require the student to make and test conjectures, using the same procedures repeatedly to find a possible solution.

Ideally, we need to spend more time where our students are thinking… more time discussing thinking questions… and focus more on the important relationships/connections that will arise through working on these problems.

Final Thoughts

Somehow we need to find the right balance between using the 4 types of questions above, however, we need to recognize that most textbooks, most teacher-made assessments, and most online resources focus heavily (if not exclusively) on knowledge and occasionally application. The balance is way off!

Focusing on being able to monitor our own types of questions isn’t enough though. We need to recognize that relationships/connections between concepts/representations are at the heart of expecting more from our students. We need to know that thinking and reasoning are HOW our students should be learning. We need to confront practices that stand in the way of us moving toward understanding and thinking, and set aside resources that focus mainly on knowledge or application. If we want to make strides forward, we need to find resources that will help US understand the material deeper and provide us with good examples.

Questions to Reflect on:

• What did your last quiz or test or exit card look like? What is your current balance of question types?
• What resources do you use? What balance do they have?
• Where do you go to find better Understanding or Thinking questions?
• What was the last problem you did that made you interested in solving it? What was it about that problem that made you interested? Likely it was a Thinking question. What was it about that problem that made it interesting?
• Much of the work related to filling gaps, intervention, assessment driving learning… points teachers toward students’ missing knowledge. How can we focus our attention more toward understanding and thinking given this reality?
• How can we better define “mastery” given the 4 categories above? Mastery must be seen as more than getting a bunch of simple knowledge questions correct!
• Who do you turn to to help you think more about the questions you ask? What professional relationships might be helpful for you?

If you haven’t already, please take a look at Marian Small’s entire presentation where she labels understanding and thinking as the “fundamentals of mathematics”

I’d love to continue the conversation about the questions we ask of our students.  Leave a comment here or on Twitter @MarkChubb3

“Making Math Visual”

A few days ago I had the privilege of presenting at OAME in Ottawa on the topic of “Making Math Visual”.   If interested, here are some of my talking points for you to reflect on:

To get us started, we discussed an image created by Christopher Danielson and asked the group what they noticed:

We noticed quite a lot in the image… and did a “how many” activity sharing various numbers we saw in the image.  After our discussions I explained that I had shared the same picture with a group of parents at a school’s parent night followed by the next picture.

The picture above was more difficult for us as teachers to see the mathematics. While we, as math teachers, saw patterns in the placements of utensils, shapes and angles around the room, quantities of countable items, multiplicative relationships between utensils and place settings, volume of wine glasses, differences in heights of chairs, perimeter around the table…..  the group correctly guessed that many parents do not typically notice the mathematics around them.

So, my suggestion for the teachers in the room was to help change this:

While I think it is important that we tackle the idea of seeing the world around us as being mathematical, a focus on making math visual needs to by MUCH more than this. To illustrate the kinds of visuals our students need to be experiencing, we completed a simple task independently:

After a few minutes of thinking, we discussed research of the different ways we use fractions, along with the various visuals that are necessary for our students to explore in order for them to develop as fractional thinkers:

• 

• 

• 

• 

• 

• 

When we looked at the ways we typically use fractions, it’s easy to notice that WE, as teachers, might need to consider how a focus on representations might help us notice if we are providing our students with a robust (let’s call this a “relational“) view of the concepts our students are learning about.

Data taken from 1 school’s teachers:

Above you see the 6 ways of visualizing fractions, but if you zoom in, you will likely notice that much of the “quotient” understanding doesn’t include a visual at all… Really, the vast majority of fractional representations here from this school were “Part – Whole relationships (continuous) models”. If, our goal is to “make math visual” then I believe we really need to spend more time considering WHICH visuals are going to be the most helpful and how those models progress over time!

We continued to talk about Liping Ma’s work where she asked teachers to answer and represent the following problem:

As you can see, being able to share a story or visual model for certain mathematics concepts seems to be a relative need. My suggestion was to really consider how a focus on visual models might be a place we can ALL learn from.

We then followed by a quick story of when a student told me that the following statement is true (click here for the full story) and my learning that came from it!

So, why should we focus on making math visual?

---

We then explored a statement that Jo Boaler shared in her Norms document:

…and I asked the group to consider if there is something we learn in elementary school that can’t be represented visually?

If you have an idea to the previous question, I’d love to hear it, because none of us could think of a concept that can’t be represented visually.

---

I then shared a quick problem that grade 7 students in one of my schools had done (see here for the description):

Along with a few different responses that students had completed:

Most of the students in the class had responded much like the image above.  Most students in the class had confused linear metric relationships (1 meter = 100 cm) with metric units of area (1 meter squared is NOT the same as 100cm2).

In fact, only two students had figured out the correct answer… which makes sense, since the students in the class didn’t learn about converting units of area through visuals.

If you are wanting to help think about HOW to “make math visual”, below is some of the suggestions we shared:

And finally some advice about what we DON’T mean when talking about making mathematics visual:

You might recognize the image above from Graham Fletcher’s post/video where he removed all of the fractional numbers off each face in an attempt to make sure that the tools were used to help students learn mathematics, instead of just using them to get answers.

---

I want to leave you with a few reflective questions:

• Can all mathematics concepts in elementary be represented visually?
• Why might a visual representation be helpful?
• If a student can get a correct answer, but can’t represent what is going on, do they really “understand” the concept?
• Are some representations more helpful than others?
• How important is it that our students notice the mathematics around them?
• How might a focus on visual representations help both us and our students deepen our understanding of the mathematics we are teaching/learning?
• Where do you turn to help you learn more about or get specific examples of how to effectively use visuals?

I’d love to continue the conversation.  Feel free to write a response, or send me a message on Twitter ( @markchubb3 ).

---

If you are interested in all of the slides, you can take a look here

Reasoning & Proving

This week I had the pleasure to see Dan Meyer, Cathy Fosnot and Graham Fletcher at OAME’s Leadership conference.

Each of the sessions were inspiring and informative… but halfway through the conference I noticed a common message that the first 2 keynote speakers were suggesting:

Dan Meyer showed us several examples of what mathematical surprise looks like in mathematics class (so students will be interested in making sense of what they are learning, and to get our students really thinking), while Cathy Fosnot shared with us how important it is for students to be puzzled in the process of developing as young mathematicians.  Both messages revolved around what I would consider the most important Process Expectation in the Ontario curriculum – Reasoning and Proving.

---

Reasoning and Proving

While some see Reasoning and Proving as being about how well an answer is constructed for a given problem – how well communicated/justified a solution is – this is not at all how I see it.  Reasoning is about sense-making… it’s about generalizing why things work… it’s about knowing if something will always, sometimes or never be true…it is about the “that’s why it works” kinds of experiences we want our students engaged in.  Reasoning is really what mathematics is all about.  It’s the pursuit of trying to help our students think mathematically (hence the name of my blog site).

---

A Non-Example of Reasoning and Proving

In the Ontario curriculum, students in grade 7 are expected to be able to:

• identify, through investigation, the minimum side and angle information (i.e.,side-side-side; side-angle-side; angle-side-angle) needed to describe a unique triangle

Many textbooks take an expectation like this and remove the need for reasoning.  Take a look:

As you can see, the textbook here shares that there are 3 “conditions for congruence”.  It shares the objective at the top of the page.  Really there is nothing left to figure out, just a few questions to complete.  You might also notice, that the phrase “explain your reasoning” is used here… but isn’t used in the sense-making way suggested earlier… it is used as a synonym for “show your work”.  This isn’t reasoning!  And there is no “identifying through investigation” here at all – as the verbs in our expectation indicate!

---

A Example of Reasoning and Proving

Instead of starting with a description of which sets of information are possible minimal information for triangle congruence, we started with this prompt:

Given a few minutes, each student created their own triangles, measured the side lengths and angles, then thought of which 3 pieces of information (out of the 6 measurements they measured) they would share.  We noticed that each successful student either shared 2 angles, with a side length in between the angles (ASA), or 2 side lengths with the angle in between the sides (SAS).  We could have let the lesson end there, but we decided to ask if any of the other possible sets of 3 pieces of information could work:

While most textbooks share that there are 3 possible sets of minimal information, 2 of which our students easily figured out, we wondered if any of the other sets listed above will be enough information to create a unique triangle.  Asking the original question didn’t offer puzzlement or surprise because everyone answered the problem without much struggle.  As math teachers we might be sure about ASA, SAS and SSS, but I want you to try the other possible pieces of information yourself:

Create triangle ABC where AB=8cm, BC=6cm, ∠BCA=60°

Create triangle FGH where ∠FGH=45°, ∠GHF=100°, HF=12cm

Create triangle JKL where ∠JKL=30°, ∠KLJ=70°, ∠LJK=80°

If you were given the information above, could you guarantee that everyone would create the exact same triangles?  What if I suggested that if you were to provide ANY 4 pieces of information, you would definitely be able to create a unique triangle… would that be true?  Is it possible to supply only 2 pieces of information and have someone create a unique triangle?  You might be surprised here… but that requires you to do the math yourself:)

---

Final Thoughts

Graham Fletcher in his closing remarks asked us a few important questions:

• Are you the kind or teacher who teaches the content, then offers problems (like the textbook page in the beginning)?  Or are you the kind of teacher who uses a problem to help your students learn?
• How are you using surprise or puzzlement in your classroom?  Where do you look for ideas?
• If you find yourself covering information, instead of helping your students learn to think mathematically, you might want to take a look at resources that aim to help you teach THROUGH problem solving (I got the problem used here in Marian Small’s new Open Questions resource).  Where else might you look?
• What does Day 1 look like when learning a new concept?
• Do you see Reasoning and Proving as a way to have students to show their work (like the textbook might suggest) or do you see Reasoning and Proving as a process of sense-making (as Marian Small shares)?
• Do your students experience moments of cognitive disequilibrium… followed by time for them to struggle independently or with a partner?  Are they regularly engaged in sense-making opportunities, sharing their thinking, debating…?
• The example I shared here isn’t the most flashy example of surprise, but I used it purposefully because I wanted to illustrate that any topic can be turned into an opportunity for students to do the thinking.  I would love to discuss a topic that you feel students can’t reason through… Let’s think together about if it’s possible to create an experience where students can experience mathematical surprise… or puzzlement… or be engaged in sense-making…  Let’s think together about how we can make Reasoning and Proving a focus for you and your students!

I’d love to continue the conversation.  Write a response, or send me a message on Twitter ( @markchubb3 ).

Reasoning and Proving

This week I had the pleasure to see Dan Meyer, Cathy Fosnot and Graham Fletcher at OAME’s Leadership conference.

Each of the sessions were inspiring and informative… but halfway through the conference I noticed a common message that the first 2 keynote speakers were suggesting:

Dan Meyer showed us several examples of what mathematical surprise looks like in mathematics class (so students will be interested in making sense of what they are learning), while Cathy Fosnot shared with us how important it is for students to be puzzled in the process of developing as young mathematicians.  Both messages revolved around what I would consider the most important Process Expectation in the Ontario curriculum – Reasoning and Proving.

---

Reasoning and Proving

While some see Reasoning and Proving as being about how well an answer is constructed for a given problem – how well communicated/justified a solution is – this is not at all how I see it.  Reasoning is about sense-making… it’s about generalizing why things work… it’s about knowing if something will always, sometimes or never be true…it is about the “that’s why it works” kinds of experiences we want our students engaged in.  Reasoning is really what mathematics is all about.  It’s the pursuit of trying to help our students think mathematically (hence the name of my blog site).

---

A Non-Example of Reasoning and Proving

In the Ontario curriculum, students in grade 7 are expected to be able to:

• identify, through investigation, the minimum side and angle information (i.e.,side-side-side; side-angle-side; angle-side-angle) needed to describe a unique triangle

Many textbooks take an expectation like this and remove the need for reasoning.  Take a look:

As you can see, the textbook here shares that there are 3 “conditions for congruence”.  It shares the objective at the top of the page.  Really there is nothing left to figure out, just a few questions to complete.  You might also notice, that the phrase “explain your reasoning” is used here… but isn’t used in the sense-making way suggested earlier… it is used as a synonym for “show your work”.  This isn’t reasoning!  And there is no “identifying through investigation” here at all – as the verbs in our expectation indicate!

---

A Example of Reasoning and Proving

Instead of starting with a description of which sets of information are possible minimal information for triangle congruence, we started with this prompt:

Given a few minutes, each student created their own triangles, measured the side lengths and angles, then thought of which 3 pieces of information (out of the 6 measurements they measured) they would share.  We noticed that each successful student either shared 2 angles, with a side length in between the angles (ASA), or 2 side lengths with the angle in between the sides (SAS).  We could have let the lesson end there, but we decided to ask if any of the other possible sets of 3 pieces of information could work:

While most textbooks share that there are 3 possible sets of minimal information, 2 of which our students easily figured out, we wondered if any of the other sets listed above will be enough information to create a unique triangle.  Asking the original question didn’t offer puzzlement or surprise because everyone answered the problem without much struggle.  As math teachers we might be sure about ASA, SAS and SSS, but I want you to try the other possible pieces of information yourself:

Create triangle ABC where AB=8cm, BC=6cm, ∠BCA=60°

Create triangle FGH where ∠FGH=45°, ∠GHF=100°, HF=12cm

Create triangle JKL where ∠JKL=30°, ∠KLJ=70°, ∠LJK=80°

If you were given the information above, could you guarantee that everyone would create the exact same triangles?  What if I suggested that if you were to provide ANY 4 pieces of information, you would definitely be able to create a unique triangle… would that be true?  Is it possible to supply only 2 pieces of information and have someone create a unique triangle?  You might be surprised here… but that requires you to do the math yourself:)

---

Final Thoughts

Graham Fletcher in his closing remarks asked us a few important questions:

• Are you the kind or teacher who teaches the content, then offers problems (like the textbook page in the beginning)?  Or are you the kind of teacher who uses a problem to help your students learn?
• How are you using surprise or puzzlement in your classroom?  Where do you look for ideas?
• If you find yourself covering information, instead of helping your students learn to think mathematically, you might want to take a look at resources that aim to help you teach THROUGH problem solving (I got the problem used here in Marian Small’s new Open Questions resource).  Where else might you look?
• What does Day 1 look like when learning a new concept?
• Do you see Reasoning and Proving as a way to have students to show their work (like the textbook might suggest) or do you see Reasoning and Proving as a process of sense-making (as Marian Small shares)?
• Do your students experience moments of cognitive disequilibrium… followed by time for them to struggle independently or with a partner?  Are they regularly engaged in sense-making opportunities, sharing their thinking, debating…?
• The example I shared here isn’t the most flashy example of surprise, but I used it purposefully because I wanted to illustrate that any topic can be turned into an opportunity for students to do the thinking.  I would love to discuss a topic that you feel students can’t reason through… Let’s think together about if it’s possible to create an experience where students can experience mathematical surprise… or puzzlement… or be engaged in sense-making…  Let’s think together about how we can make Reasoning and Proving a focus for you and your students!

I’d love to continue the conversation.  Write a response, or send me a message on Twitter ( @markchubb3 ).

Making Math Visual

A few days ago I had the privilege of presenting at MAC2 to a group of teachers in Orillia on the topic of “Making Math Visual”.   If interested, here are some of my talking points for you to reflect on:

To get us started I shared an image created by Christopher Danielson and asked the group what they noticed:

We noticed quite a lot in the image… and did a “how many” activity sharing various numbers we saw in the image.  After our discussions I explained that I had shared the same picture with a group of parents at a school’s parent night followed by the next picture.

I asked the group of teachers what mathematics they noticed here… then how they believed parents might have answered the question.  While we, as math teachers, saw patterns in the placements of utensils, shapes and angles around the room, quantities of countable items, multiplicative relationships between utensils and place settings, volume of wine glasses, differences in heights of chairs, perimeter around the table…..  the group correctly guessed that many parents do not typically notice the mathematics around them.

So, my suggestion for the teachers in the room was to help change this:

I then asked the group to do a simple task for us to learn from:

After a few minutes of thinking, I shared some research of the different ways we use fractions:

When we looked at the ways we typically use fractions, it’s easy to notice that WE, as teachers, might need to consider how a focus on representations might help us notice if we are providing our students with a robust (let’s call this a “relational“) view of the concepts our students are learning about.

Data taken from 1 school’s teachers:

We continued to talk about Liping Ma’s work where she asked teachers to answer and represent the following problem:

Followed by a quick story of when a student told me that the following statement is true (click here for the full story).

So, why should we focus on making math visual?

---

We then explored a statement that Jo Boaler shared in her Norms document:

…and I asked the group to consider if there is something we learn in elementary school that can’t be represented visually?

If you have an idea to the previous question, I’d love to hear it, because none of us could think of a concept that can’t be represented visually.

---

I then shared a quick problem that grade 7 students in one of my schools had done (see here for the description):

Along with a few different responses that students had completed:

Most of the students in the class had responded much like the image above.  Most students in the class had confused linear metric relationships (1 meter = 100 cm) with metric units of area (1 meter squared is NOT the same as 100cm2).

In fact, only two students had figured out the correct answer… which makes sense, since the students in the class didn’t learn about converting units of area through visuals.

We wrapped up with a few suggestions:

And finally some advice about what we DON’T mean when talking about making mathematics visual:

You might recognize the image above from Graham Fletcher’s post/video where he removed all of the fractional numbers off each face in an attempt to make sure that the tools were used to help students learn mathematics, instead of just using them to get answers.

---

I want to leave you with a few reflective questions:

• Can all mathematics concepts in elementary school be represented visually?
• Why might a visual representation be helpful?
• Are some representations more helpful than others?
• How important is it that our students notice the mathematics around them?
• How might a focus on visual representations help both us and our students deepen our understanding of the mathematics we are teaching/learning?

I’d love to continue the conversation.  Feel free to write a response, or send me a message on Twitter ( @markchubb3 ).

---

If you are interested in all of the slides, you can take a look here

 

 

Developing Spatial Reasoning through Guided Play

For the last few months, a team of kindergarten teachers and myself have been working together to deepen our understanding of early years mathematics, spatial reasoning, and the importance of guided play as a vehicle to engage our students to think mathematically.  Below is a copy of our slideshow presentation we shared at OAME 2017, and some of the documents we have created over the past few months.

A quick synopsis of our work first:

While our research led us toward Doug Clement’s work about trajectories, and research about spatial reasoning and early mathematics, much of the tasks we actually did with students directly came from the book shown above (Taking Shape) which I can’t recommend enough – if you can, get yourself a copy!

---

We discussed the quote above to help us realize what actually underpins mathematics success.  More details about how the quote ends here.

---

We shared research showing just how important early mathematics is, and specifically what the kinds of instruction could / should look like to accomplish this learning.  Duncan et. al., is a widely quoted piece of research that has led many to realize that early math learning needs to be a focus in schools – even more so than early reading!

---

We played a few games that helped us stretch our spatial reasoning abilities.  The image above was part of our “See It, Build It, Check It” activity (found in Taking Shape).  Everyone saw the image for a minute, then was asked to build it once the image was removed.  What we noticed is just how difficult spatial tasks are for us!

---

 

After we had the opportunity to play for a bit, we dug back into the research about spatial reasoning and the jobs typically chosen based on (high school) spatial ability.  Hopefully you noticed something interesting on the graph above!

So, we know how important spatial reasoning is, but the 3 pieces above (taken from Paying Attention to Spatial Reasoning document) might help us realize how important a focus on spatial reasoning is for both our students and us.

---

In our time together, we learned a lot about the importance of observing our students as they were engaged in the learning.  From the initial choices they made, to how they overcame obstacles, to understanding the mental actions that were happening… Observing students in the moment is far more powerful than collecting correct answers!

See the link at the bottom of the page for our connections to Doug Clements’ work.

---

We also discussed the specific connections between the mathematics behaviours and the learning that happened beyond.  In our Kindergarten program document, our students’ expectations fall under 4 frames (see above) so we linked the learning we saw to the program document in a way that helps us see the depth and breadth of the kindergarten program (see document linked below).

---

We then ended our presentation with a synopsis of what we learned throughout our work together.  While the slideshow might be helpful here (I’d love for someone to comment on those slides at the end), the conversations that Sue, Kristi and Kristen had with others have shown me just how valuable it is to spend time learning together.  I couldn’t be prouder to be able to work with such reflective and dedicated teachers!

---

Our presentation:

Guided Play Slideshow

A few of our handouts:

4 Frames handout

Developmental Trajectories – Adapted from Doug Clements’ work

Spatial Language

---

As always, I’d love to hear about your thoughts or comments.  Leave a comment below or catch us on Twitter:

@MarkChubb3

@mrs_dt

@mrs_penlington

@kristinWillms